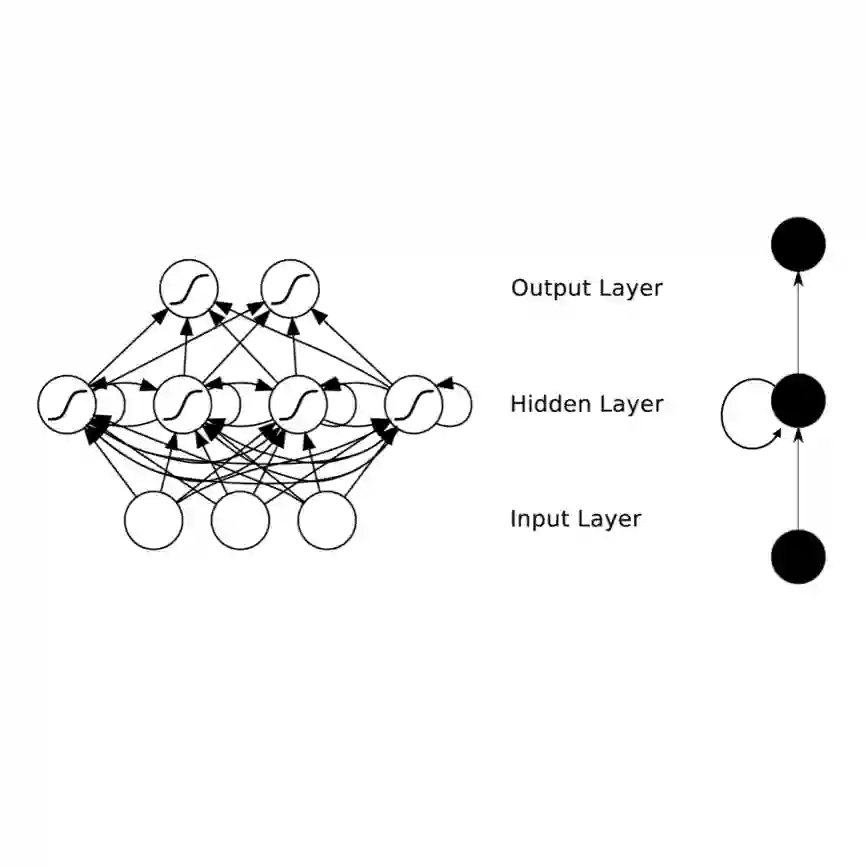
Counter machines have achieved a newfound relevance to the field of natural language processing (NLP): recent work suggests some strong-performing recurrent neural networks utilize their memory as counters. Thus, one potential way to understand the success of these networks is to revisit the theory of counter computation. Therefore, we study the abilities of real-time counter machines as formal grammars, focusing on formal properties that are relevant for NLP models. We first show that several variants of the counter machine converge to express the same class of formal languages. We also prove that counter languages are closed under complement, union, intersection, and many other common set operations. Next, we show that counter machines cannot evaluate boolean expressions, even though they can weakly validate their syntax. This has implications for the interpretability and evaluation of neural network systems: successfully matching syntactic patterns does not guarantee that counter memory accurately encodes compositional semantics. Finally, we consider whether counter languages are semilinear. This work makes general contributions to the theory of formal languages that are of potential interest for understanding recurrent neural networks.
翻译:反制机器已经取得了与自然语言处理领域(NLP)的新的相关性:最近的工作表明,一些表现强劲的经常性神经网络利用记忆作为计数器。因此,理解这些网络成功与否的一个潜在途径是重新审视反制计算理论。因此,我们研究实时反制机器作为正式语法模型的能力,重点是与自然语言处理模型相关的正式属性。我们首先显示,反制机器的若干变体会聚在一起,以表达同一类正式语言。我们还证明,反向语言在补充、联合、交叉和许多其他共同设置操作下是封闭的。接下来,我们显示反向机器无法评价布尔语表达,尽管它们能够弱化地验证其语法。这对神经网络系统的可解释性和评估有影响:成功匹配同步模式并不能保证反记忆准确地编码成成成文的语义。最后,我们考虑反向语言是否为半线性语言。这项工作对理解经常性神经网络的潜在兴趣的正式语言理论作出了一般性贡献。