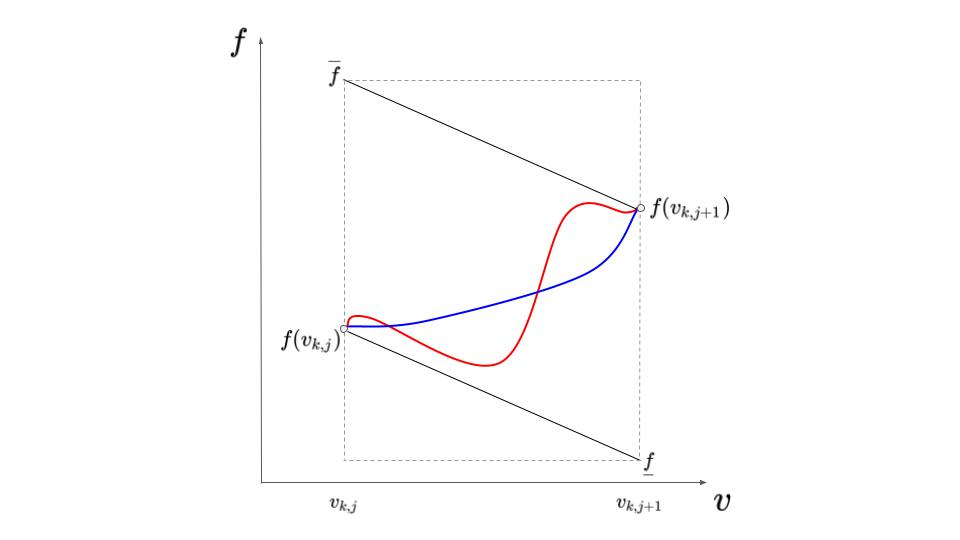
Myerson's regularity condition of a distribution is a standard assumption in economics. In this paper, we study the complexity of describing a regular distribution within a small statistical distance. Our main result is that $\tilde{\Theta}{(\epsilon^{-0.5})}$ bits are necessary and sufficient to describe a regular distribution with support $[0,1]$ within $\epsilon$ Levy distance. We prove this by showing that we can learn the regular distribution approximately with $\tilde{O}(\epsilon^{-0.5})$ queries to the cumulative density function. As a corollary, we show that the pricing query complexity to learn the class of regular distribution with support $[0,1]$ within $\epsilon$ Levy distance is $\tilde{\Theta}{(\epsilon^{-2.5})}$. To learn the mixture of two regular distributions, $\tilde{\Theta}(\epsilon^{-3})$ pricing queries are required.
翻译:暂无翻译