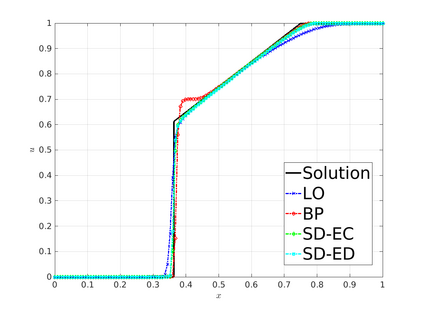
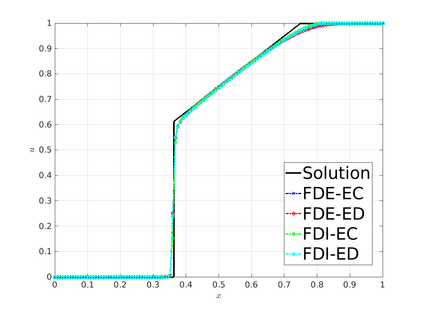
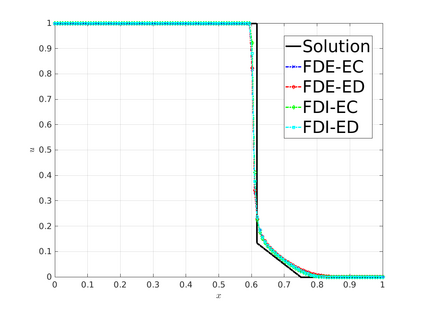
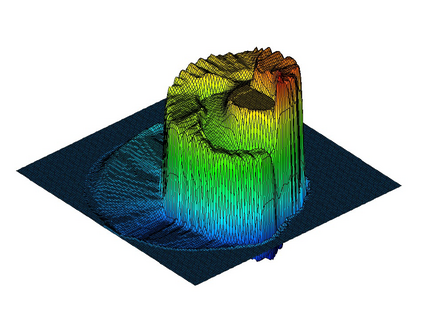
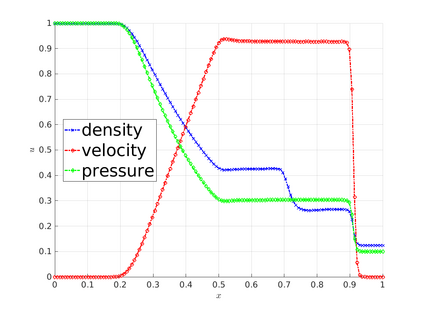
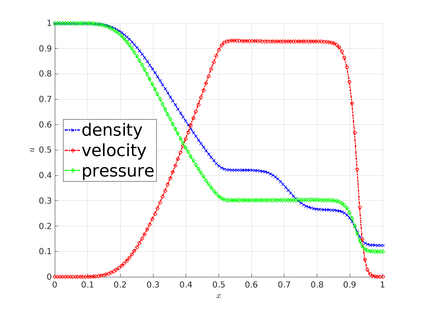
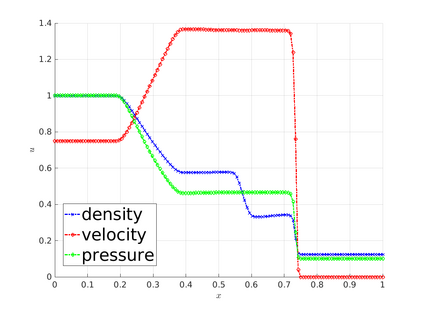
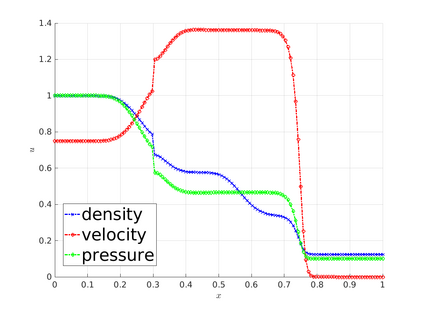
The algebraic flux correction (AFC) schemes presented in this work constrain a standard continuous finite element discretization of a nonlinear hyperbolic problem to satisfy relevant maximum principles and entropy stability conditions. The desired properties are enforced by applying a limiter to antidiffusive fluxes that represent the difference between the high-order baseline scheme and a property-preserving approximation of Lax--Friedrichs type. In the first step of the limiting procedure, the given target fluxes are adjusted in a way that guarantees preservation of local and/or global bounds. In the second step, additional limiting is performed, if necessary,to ensure the validity of fully discrete and/or semi-discrete entropy inequalities. The limiter-based entropy fixes considered in this work are applicable to finite element discretizations of scalar hyperbolic equations and systems alike. The underlying inequality constraints are formulated using Tadmor's entropy stability theory. The proposed limiters impose entropy-conservative or entropy-dissipative bounds on the rate of entropy production by antidiffusive fluxes and Runge--Kutta (RK) time discretizations. Two versions of the fully discrete entropy fix are developed for this purpose. To motivate the use of limiter-based entropy fixes, we prove a finite element version of the Lax--Wendroff theorem and perform numerical studies for standard test problems. In our numerical experiments, entropy-dissipative schemes converge to correct weak solutions of scalar conservation laws, of the Euler equations, and of the shallow water equations.
翻译:本文中介绍的藻类通量校正(AFC) 计划限制非线性双曲性问题的标准连续限制元素离散, 以满足相关最大原则和增温稳定性条件。 想要的特性通过对代表高序基线方案和拉克斯- 弗瑞德丰富方程式类型之差的抗反异通量调节器实施限值。 在限制程序的第一步, 给定目标通量的调整方式可以保证保存本地和/ 或全球界限。 第二步, 如果必要, 将执行额外的限制, 以确保完全离散和/ 或半异性变异酶不平等的有效性。 本文中考虑的基于限值的变异性通性修正适用于高压- 超离异方程式和系统等的异性元素离异性。 在限制程序的第一步中, 定值的不平等限制是使用塔德摩尔基的恒定稳定性理论理论理论。 拟议的限值将nro- 固值或正反异性变异变异变异法的内程- 系统- 的内流- 内基- 的内基- 变变变变变的内基- 机- 的内基- 流- 流- 的内基- 机- 流- 流- 的内基- 的内基- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 和- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流- 流-