Drift estimation of the threshold Ornstein-Uhlenbeck process from continuous and discrete observations

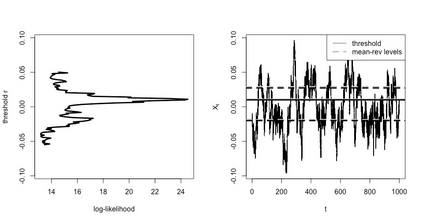
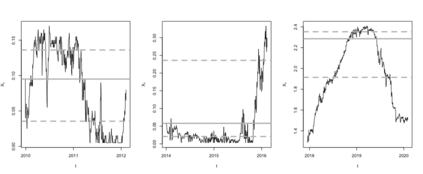
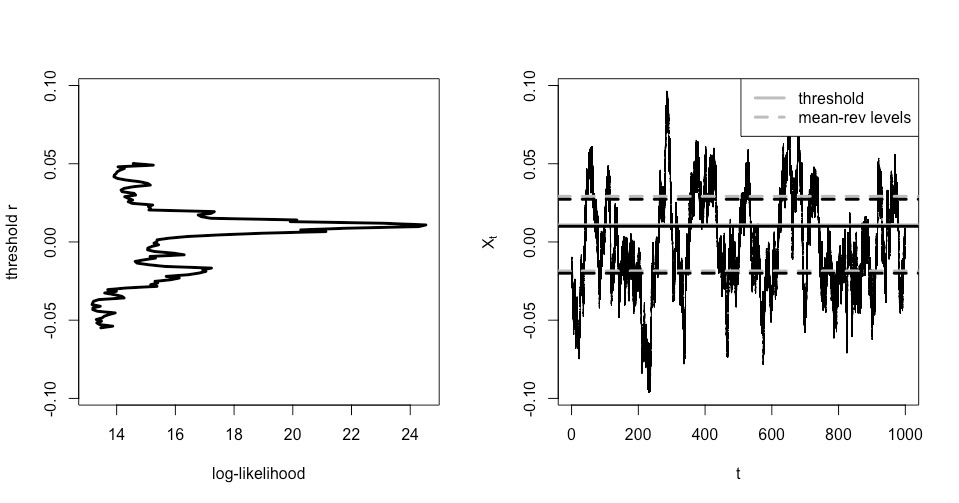
We refer by threshold Ornstein-Uhlenbeck to a continuous-time threshold autoregressive process. It follows the Ornstein-Uhlenbeck dynamics when above or below a fixed level, yet at this level (threshold) its coefficients can be discontinuous. We discuss (quasi)-maximum likelihood estimation of the drift parameters, both assuming continuous and discrete time observations. In the ergodic case, we derive consistency and speed of convergence of these estimators in long time and high frequency. Based on these results, we develop a test for the presence of a threshold in the dynamics. Finally, we apply these statistical tools to short-term US interest rates modeling.