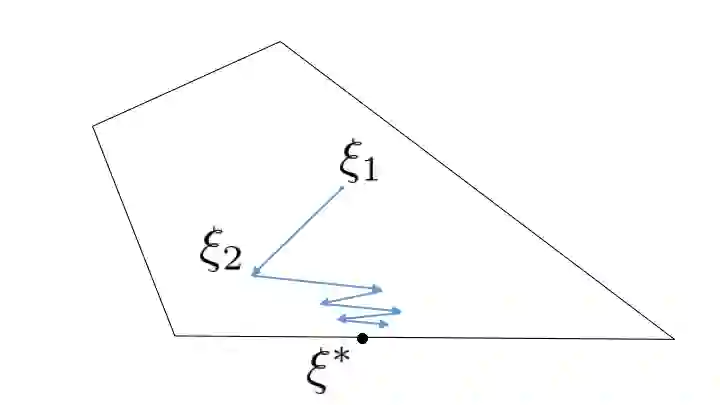
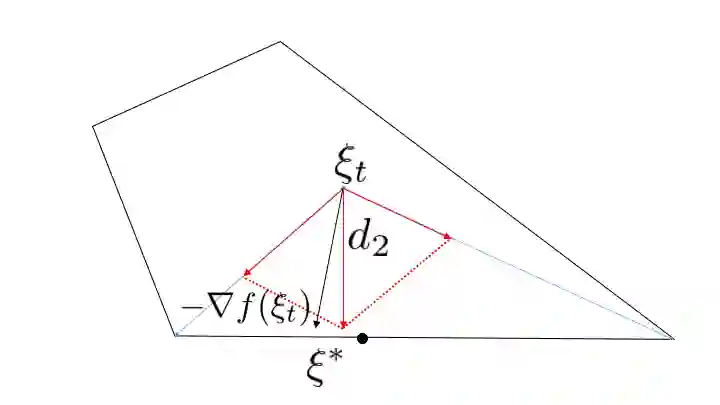
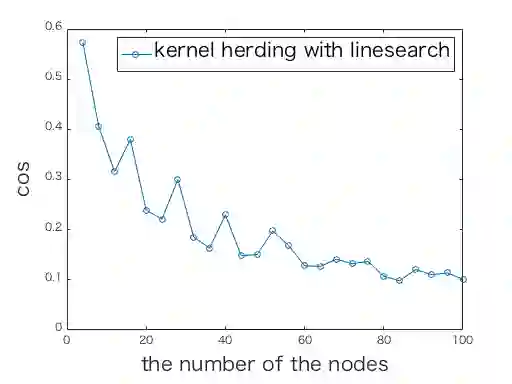
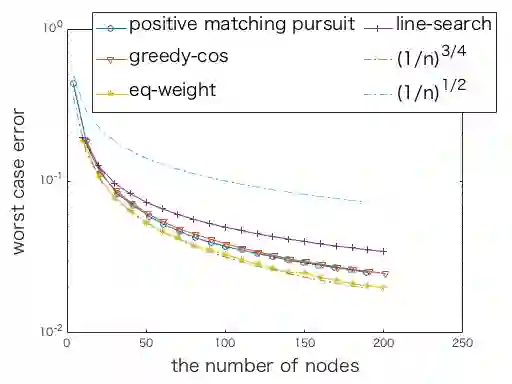
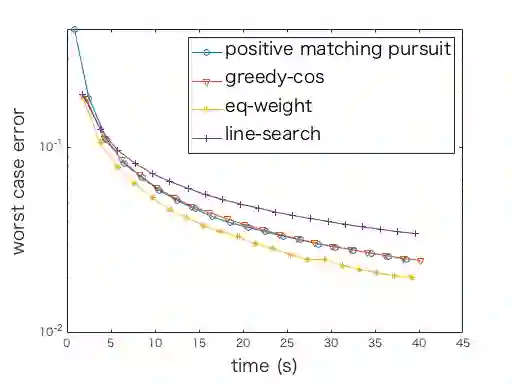
Kernel herding is a method used to construct quadrature formulas in a reproducing kernel Hilbert space. Although there are some advantages of kernel herding, such as numerical stability of quadrature and effective outputs of nodes and weights, the convergence speed of worst-case integration error is slow in comparison to other quadrature methods. To address this problem, we propose two improved versions of the kernel herding algorithm. The fundamental concept of both algorithms involves approximating negative gradients with a positive linear combination of vertex directions. We analyzed the convergence and validity of both algorithms theoretically; in particular, we showed that the approximation of negative gradients directly influences the convergence speed. In addition, we confirmed the accelerated convergence of the worst-case integration error with respect to the number of nodes and computational time through numerical experiments.
翻译:内核放牧是用来在复制内核Hilbert空间中构建二次公式的一种方法。虽然内核放牧有一些好处,例如二次的数值稳定性和节点和重量的有效输出,但最坏情况集成错误的趋同速度与其他四面形方法相比是缓慢的。为了解决这个问题,我们提出了两个改进的内核放牧算法版本。两种算法的基本概念都涉及近似负梯度和正线性垂直组合的顶点方向。我们从理论上分析了两种算法的趋同和有效性;特别是,我们表明负梯度的近似直接影响到趋同速度。此外,我们还确认,通过数字实验,最坏情况集成错误在节点数和计算时间方面加速趋同。