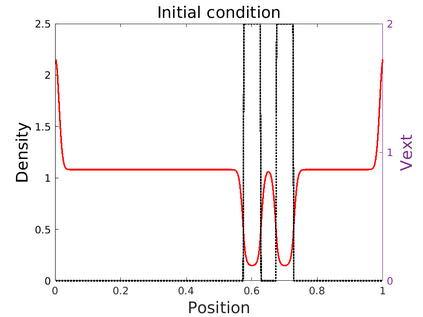
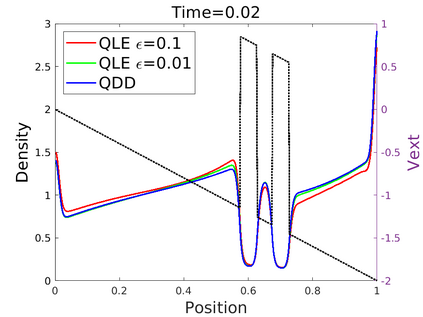
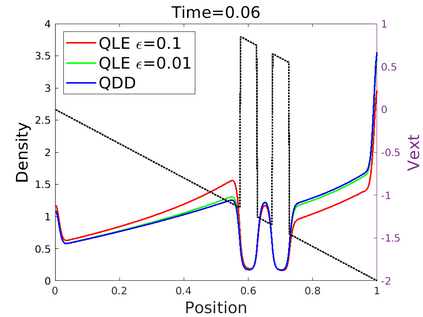
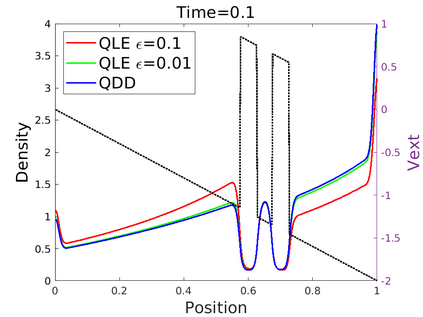
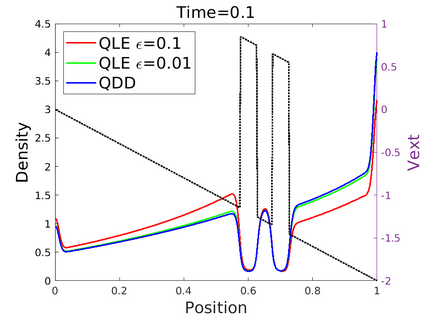
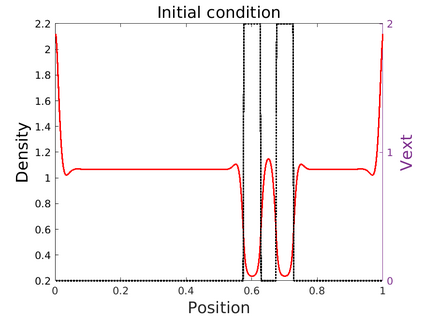
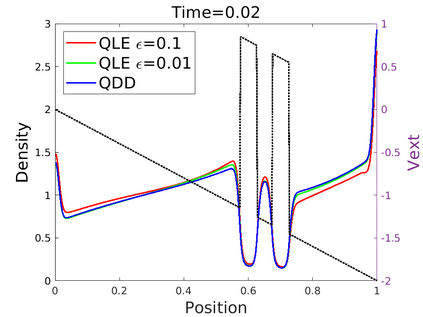
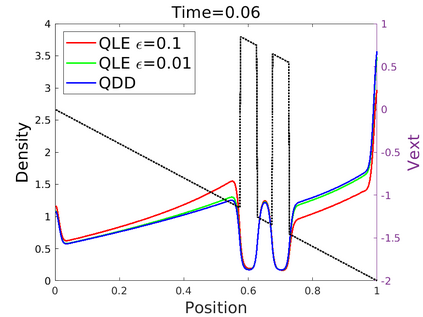
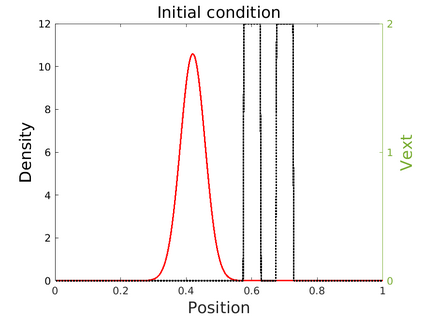
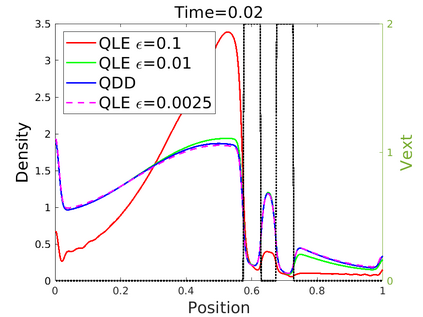
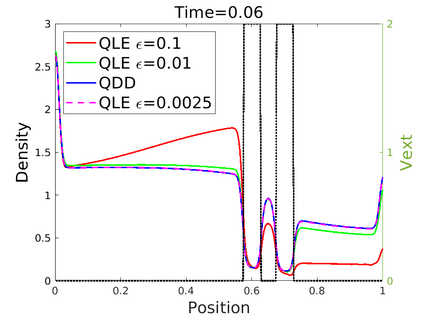
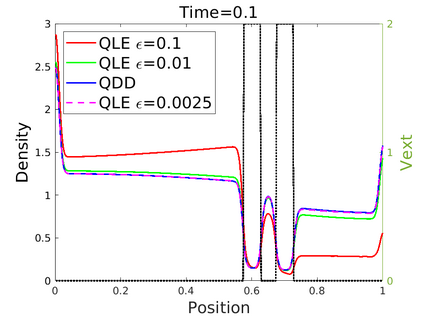
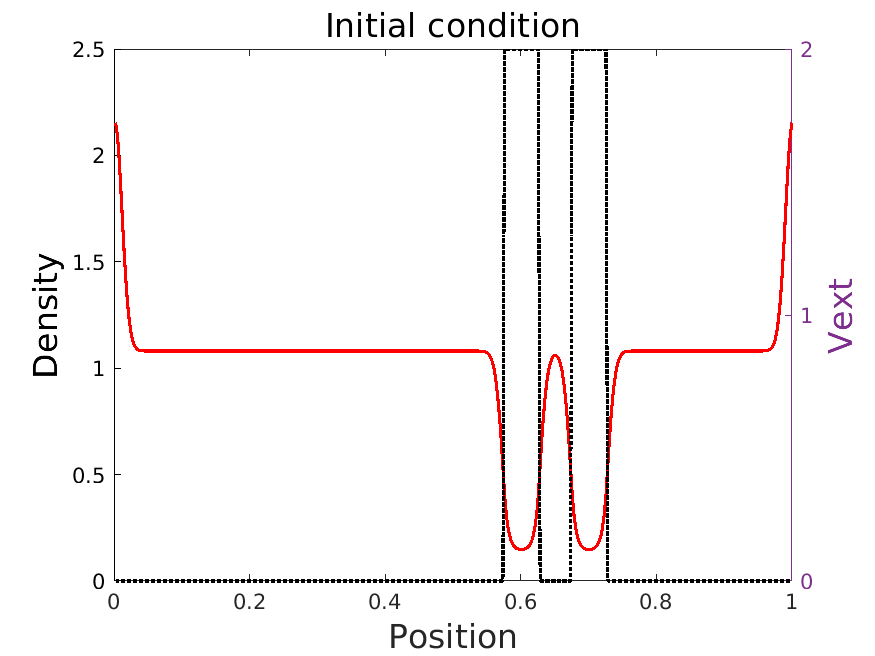
We introduce in this work an efficient numerical method for the simulation of the quantum Liouville-BGK equation, which models the diffusive transport of quantum particles. The corner stone to the model is the BGK collision operator, obtained by minimizing the quantum free energy under the constraint that the local density of particles is conserved during collisions. This leads to a large system of coupled nonlinear nonlocal PDEs whose resolution is challenging. We then define a splitting scheme that separates the transport and the collision parts, which, exploiting the local conservation of particles, leads to a fully linear collision step. The latter involves the resolution of a constrained optimization problem that is is handled with the nonlinear conjugate gradient algorithm. We prove that the time semi-discrete scheme is convergent, and as an application of our numerical scheme, we validate the quantum drift-diffusion model that is obtained as the diffusive limit of the quantum Liouville-BGK equation.
翻译:我们在这项工作中引入了一个高效的数字方法来模拟量子Liouville-BGK等式,该等式是量子粒子的显性迁移模型。该模型的转角石块是BGK碰撞操作员,该操作员通过在碰撞期间节制当地粒子密度的制约下将量子无能量最小化而获得。这导致一个庞大的非线性非局部PDE系统,其分辨率具有挑战性。然后我们定义了一个分离运输和碰撞部分的分解计划,它利用微粒的局部保护,导致一个完全线性碰撞步骤。后者涉及一个受限制的优化问题的解决,这一问题与非线性同源梯度算法一起处理。我们证明时间半分解方案是趋同的,并且作为我们数字方案的一种应用,我们验证了作为量子Louville-BGK等式的分流-分解模型获得的量流化模型。