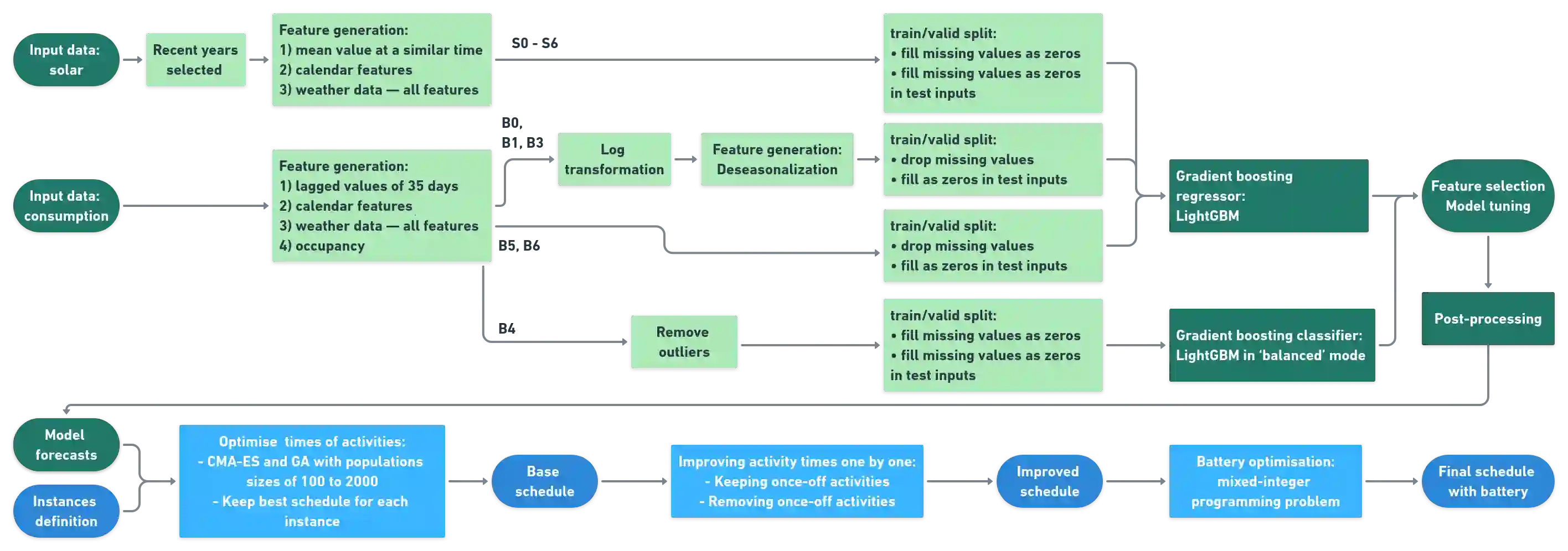
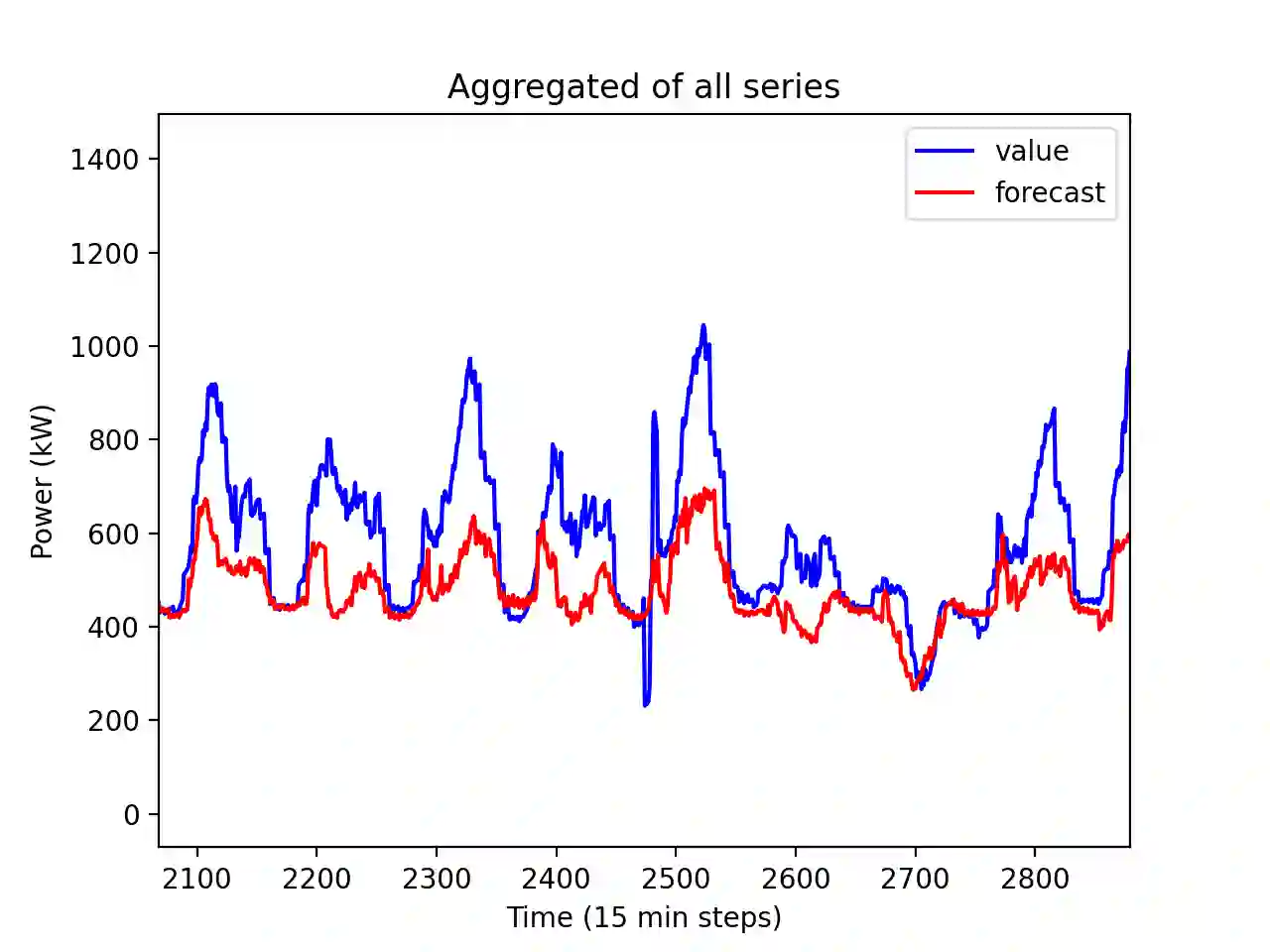
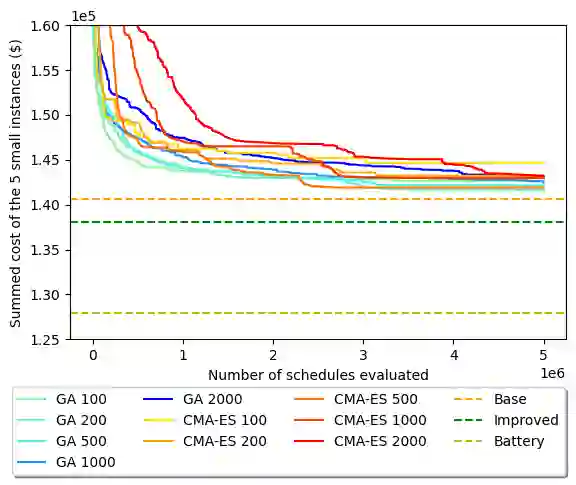
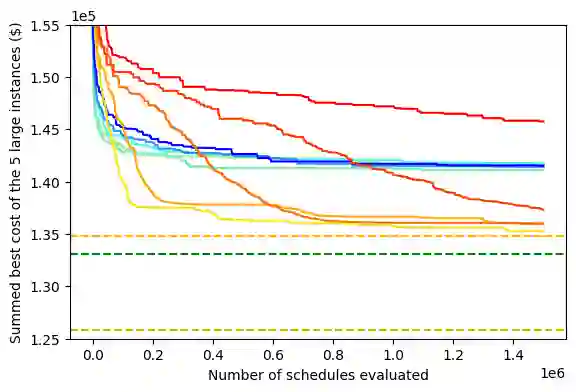
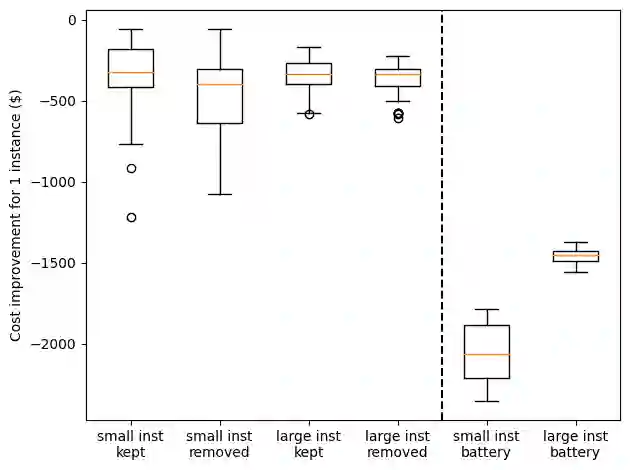
This paper presents a solution to a predict then optimise problem which goal is to reduce the electricity cost of a university campus. The proposed methodology combines a multi-dimensional time series forecast and a novel approach to large-scale optimization. Gradient-boosting method is applied to forecast both generation and consumption time-series of the Monash university campus for the month of November 2020. For the consumption forecasts we employ log transformation to model trend and stabilize variance. Additional seasonality and trend features are added to the model inputs when applicable. The forecasts obtained are used as the base load for the schedule optimisation of university activities and battery usage. The goal of the optimisation is to minimize the electricity cost consisting of the price of electricity and the peak electricity tariff both altered by the load from class activities and battery use as well as the penalty of not scheduling some optional activities. The schedule of the class activities is obtained through evolutionary optimisation using the covariance matrix adaptation evolution strategy and the genetic algorithm. This schedule is then improved through local search by testing possible times for each activity one-by-one. The battery schedule is formulated as a mixed-integer programming problem and solved by the Gurobi solver. This method obtains the second lowest cost when evaluated against 6 other methods presented at an IEEE competition that all used mixed-integer programming and the Gurobi solver to schedule both the activities and the battery use. The code and data used for the paper are publicly available.
翻译:本文为预测然后优化问题提供了一个解决方案,目标是降低大学校园的电费。拟议方法将多维时间序列预测和大规模优化的新办法结合起来。对Monash大学校园2020年11月的发电和消费时间序列都采用了渐进推动方法。对于消费预测,我们使用日志转换来模型趋势并稳定差异。在适用的情况下,在模型输入中添加更多的季节性和趋势特征。所获得的预测被用作大学活动和电池使用时间表优化的基础负荷。优化的目的是尽量减少电价和电价峰值的峰值税,这些电价由舱内活动和电池使用负荷的负荷以及不安排某些可选活动的罚款所改变而构成。对于班级活动的进度,我们采用对模型变异矩阵适应演变战略和遗传算法进行进化优化。随后,通过对每项活动进行可能的逐次测试,改进了本地搜索。电池时间表是设计由电价和电峰值电峰值税构成的电价成本,由电力价格和电峰值税构成,由类活动和电池使用电池的使用以及不安排某些可选活动加以调整。在使用 GUI 和混合计算方法时,要用最低成本,用GUI 和混合计算方法来解决了使用这一方法,然后对使用该方法进行评估。