Locally Differentially Private Sparse Vector Aggregation

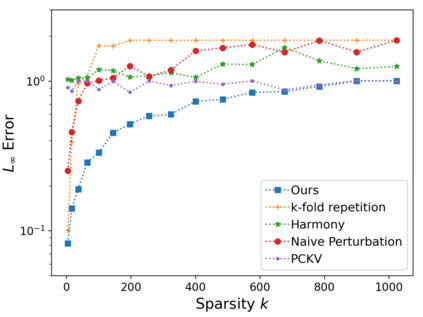
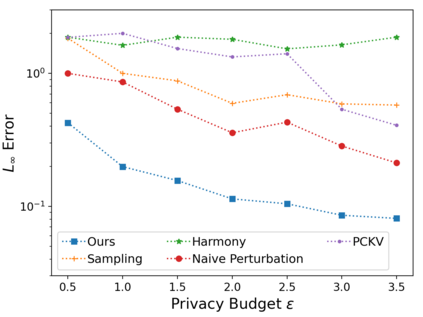
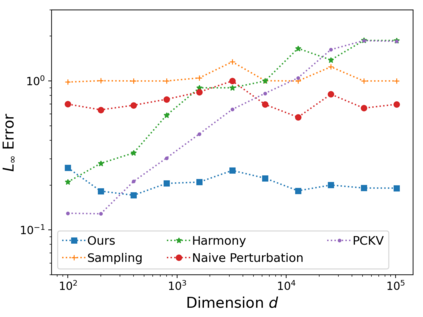
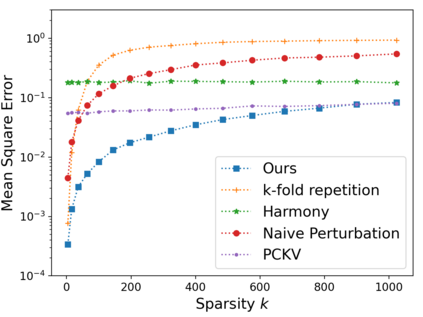
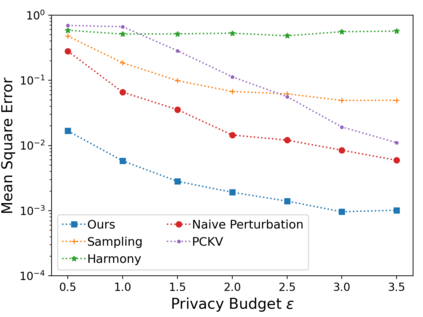
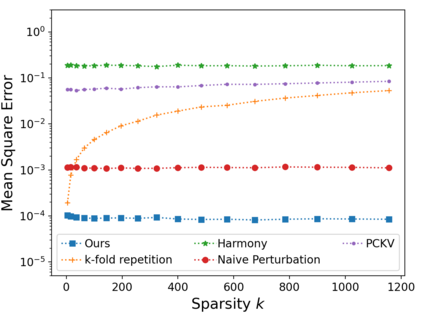
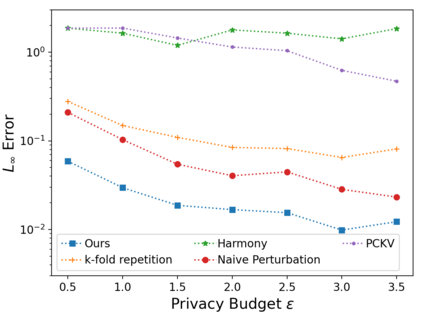
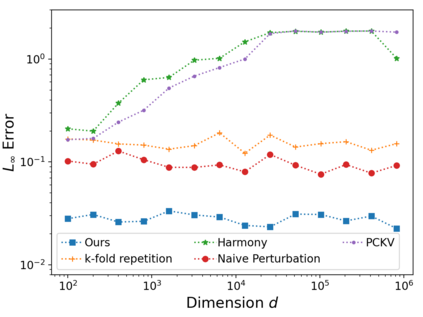
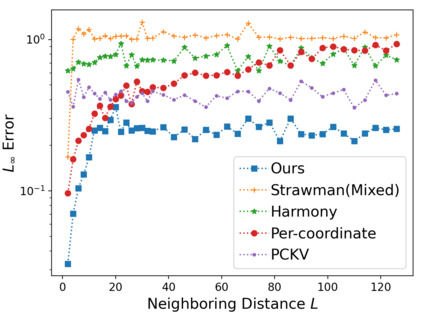
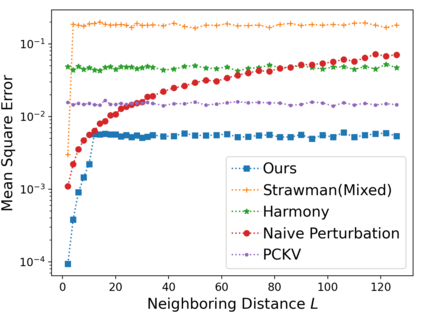
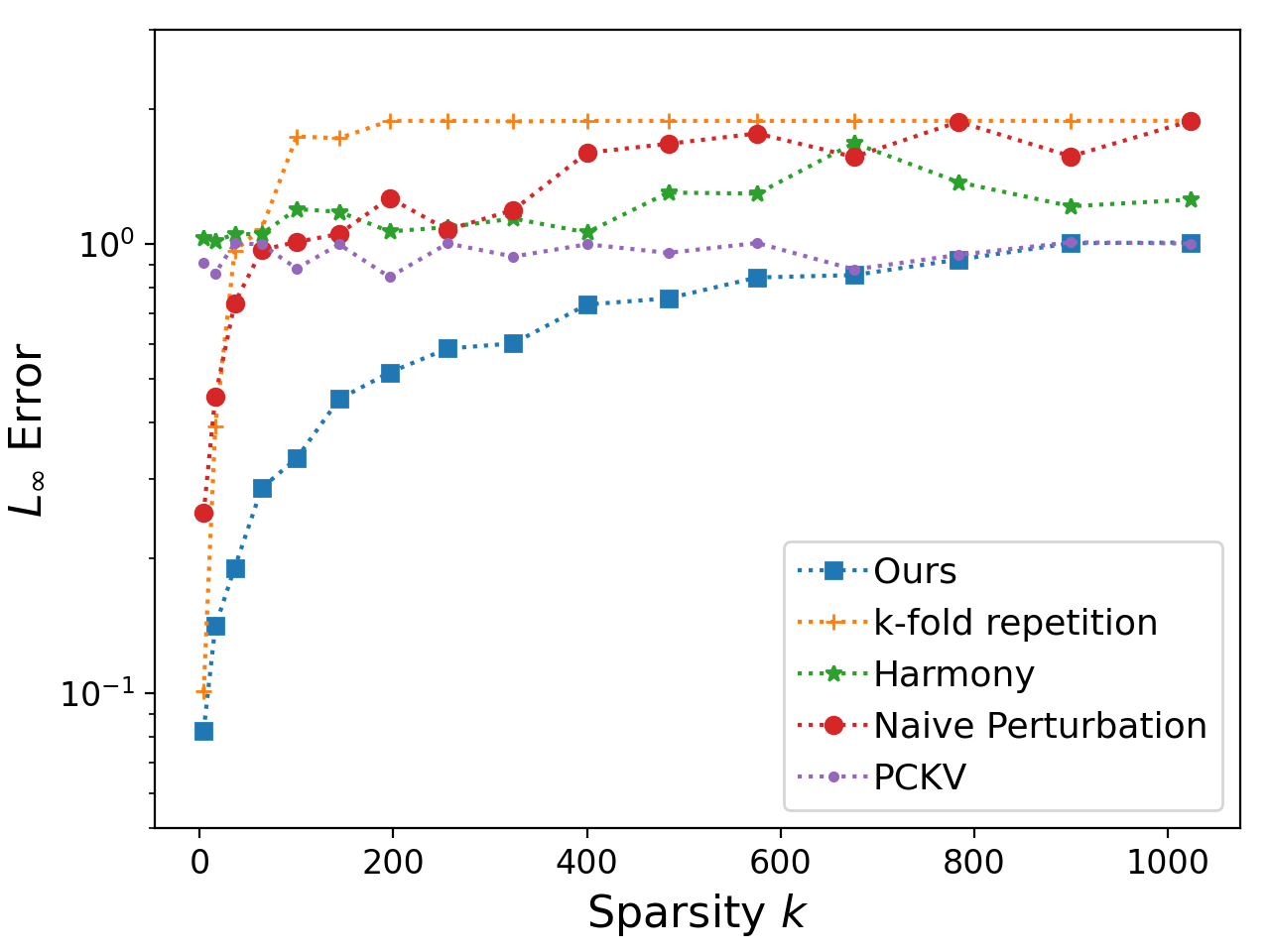
Vector mean estimation is a central primitive in federated analytics. In vector mean estimation, each user $i \in [n]$ holds a real-valued vector $v_i\in [-1, 1]^d$, and a server wants to Not only so, we would like to protect each individual user's privacy. In this paper, we consider the $k$-sparse version of the vector mean estimation problem, that is, suppose that each user's vector has at most $k$ non-zero coordinates in its $d$-dimensional vector, and moreover, $k \ll d$. In practice, since the universe size $d$ can be very large (e.g., the space of all possible URLs), we would like the per-user communication to be succinct, i.e., independent of or (poly-)logarithmic in the universe size. In this paper, we are the first to show matching upper- and lower-bounds for the $k$-sparse vector mean estimation problem under local differential privacy. Specifically, we construct new mechanisms that achieve asymptotically optimal error as well as succinct communication, either under user-level-LDP or event-level-LDP. We implement our algorithms and evaluate them on synthetic as well as real-world datasets. Our experiments show that we can often achieve one or two orders of magnitude reduction in error in comparison with prior works under typical choices of parameters, while incurring insignificant communication cost.