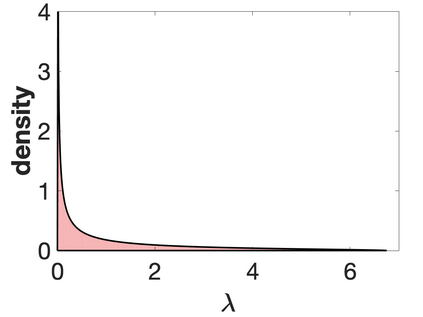
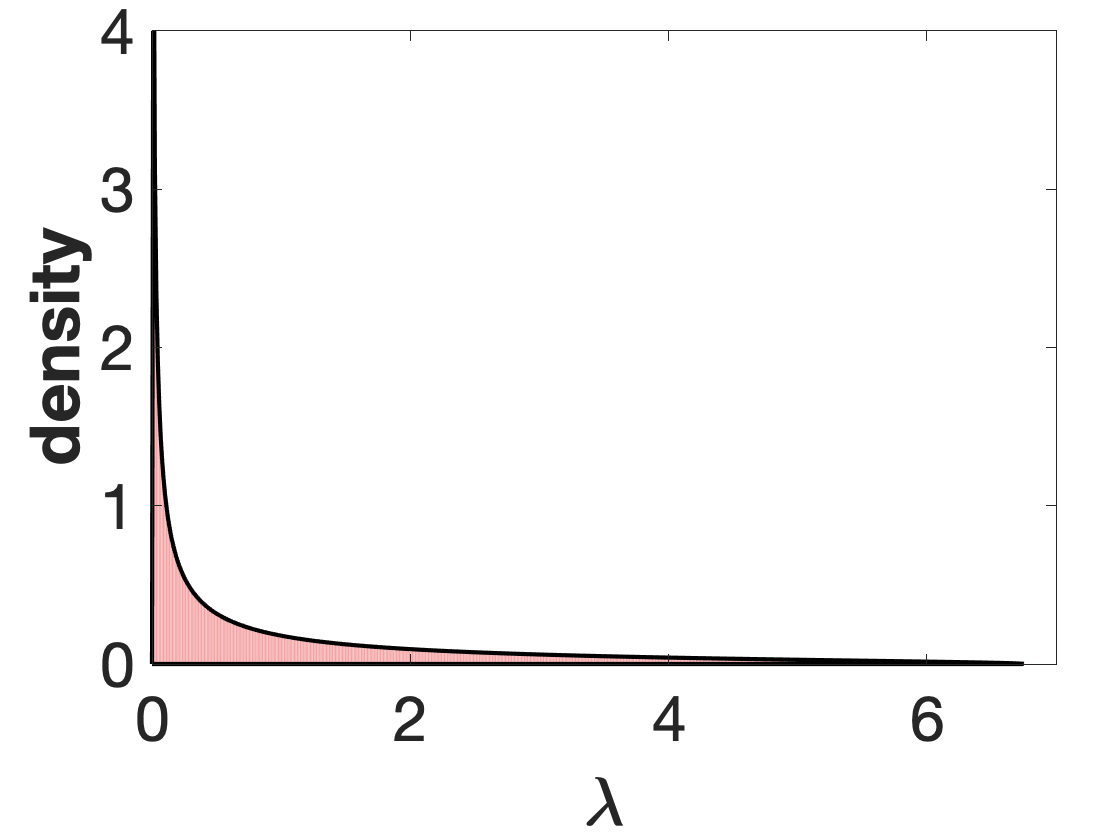
We present a simple, perturbative approach for calculating spectral densities for random matrix ensembles in the thermodynamic limit we call the Perturbative Resolvent Method (PRM). The PRM is based on constructing a linear system of equations and calculating how the solutions to these equation change in response to a small perturbation using the zero-temperature cavity method. We illustrate the power of the method by providing simple analytic derivations of the Wigner Semi-circle Law for symmetric matrices, the Marchenko-Pastur Law for Wishart matrices, the spectral density for a product Wishart matrix composed of two square matrices, and the Circle and elliptic laws for real random matrices.
翻译:我们在计算热力极限中随机矩阵组合的光谱密度时,提出了一个简单、有扰动性的方法,我们称之为 " 扰动解解析法 " (PRM),其基础是构建一个线性方程式系统,并计算出如何用零温感性电感学法的小扰动来改变这些方程式的解决方案。我们通过提供对称基体的Wigner半圆轴法、Wishart矩阵的Marchenko-Pastur法、由两个平方矩阵组成的产品Wishart矩阵的光谱密度,以及真实随机基体的圆形和椭圆法,来说明该方法的力量。