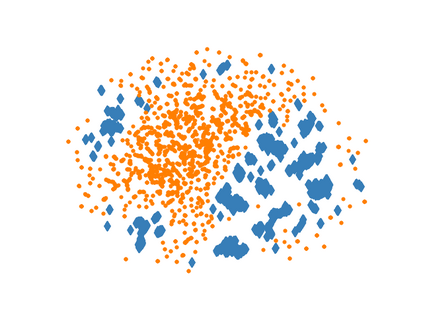
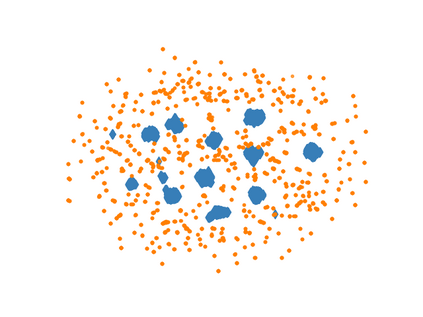
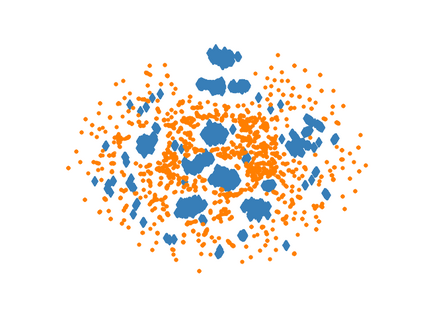
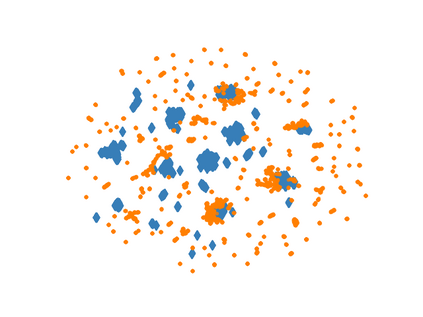
Learning representations of multimodal data that are both informative and robust to missing modalities at test time remains a challenging problem due to the inherent heterogeneity of data obtained from different channels. To address it, we present a novel Geometric Multimodal Contrastive (GMC) representation learning method comprised of two main components: i) a two-level architecture consisting of modality-specific base encoder, allowing to process an arbitrary number of modalities to an intermediate representation of fixed dimensionality, and a shared projection head, mapping the intermediate representations to a latent representation space; ii) a multimodal contrastive loss function that encourages the geometric alignment of the learned representations. We experimentally demonstrate that GMC representations are semantically rich and achieve state-of-the-art performance with missing modality information on three different learning problems including prediction and reinforcement learning tasks.
翻译:由于从不同渠道获得的数据具有固有的差异性,因此在测试时对缺少的模式进行内容丰富和健全的多式数据的学习表现仍是一个具有挑战性的问题。为了解决这一问题,我们提出了一个新型的几何多式(GMC)代表学习方法,由两个主要部分组成:(一) 由特定模式基础编码器组成的两级结构,允许将任意数量的模式处理成一个固定维度中间代表器,以及一个共同的投影头,将中间代表制绘制成一个潜在的代表空间;(二) 多式联运的对比损失功能,鼓励对所了解的表示法进行几何比对。我们实验性地表明,GMC的表示法具有内在的丰富性,并以三种不同学习问题(包括预测和加强学习任务)的缺失模式信息实现最先进的表现。