Error estimation and adaptivity for stochastic collocation finite elements Part I: single-level approximation

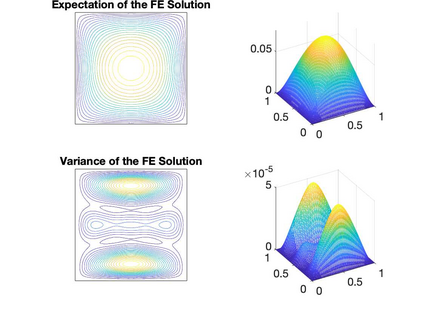
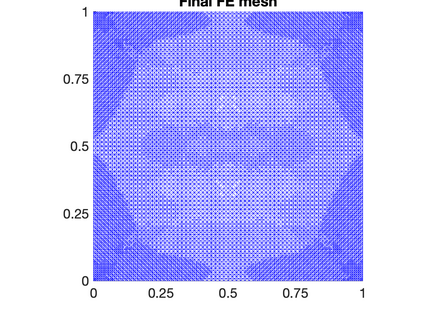
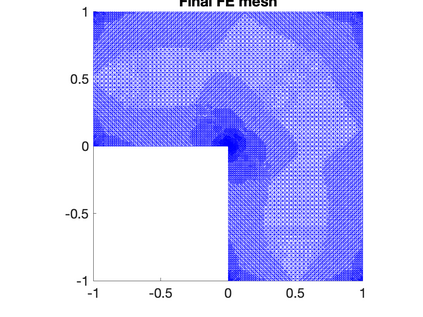
A general adaptive refinement strategy for solving linear elliptic partial differential equation with random data is proposed and analysed herein. The adaptive strategy extends the a posteriori error estimation framework introduced by Guignard and Nobile in 2018 (SIAM J. Numer. Anal., 56, 3121--3143) to cover problems with a nonaffine parametric coefficient dependence. A suboptimal, but nonetheless reliable and convenient implementation of the strategy involves approximation of the decoupled PDE problems with a common finite element approximation space. Computational results obtained using such a single-level strategy are presented in this paper (part I). Results obtained using a potentially more efficient multilevel approximation strategy, where meshes are individually tailored, will be discussed in part II of this work. The codes used to generate the numerical results are available on GitHub