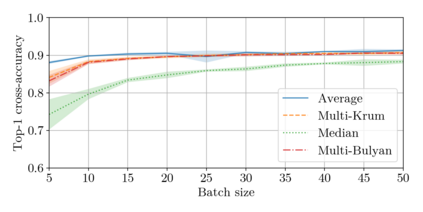
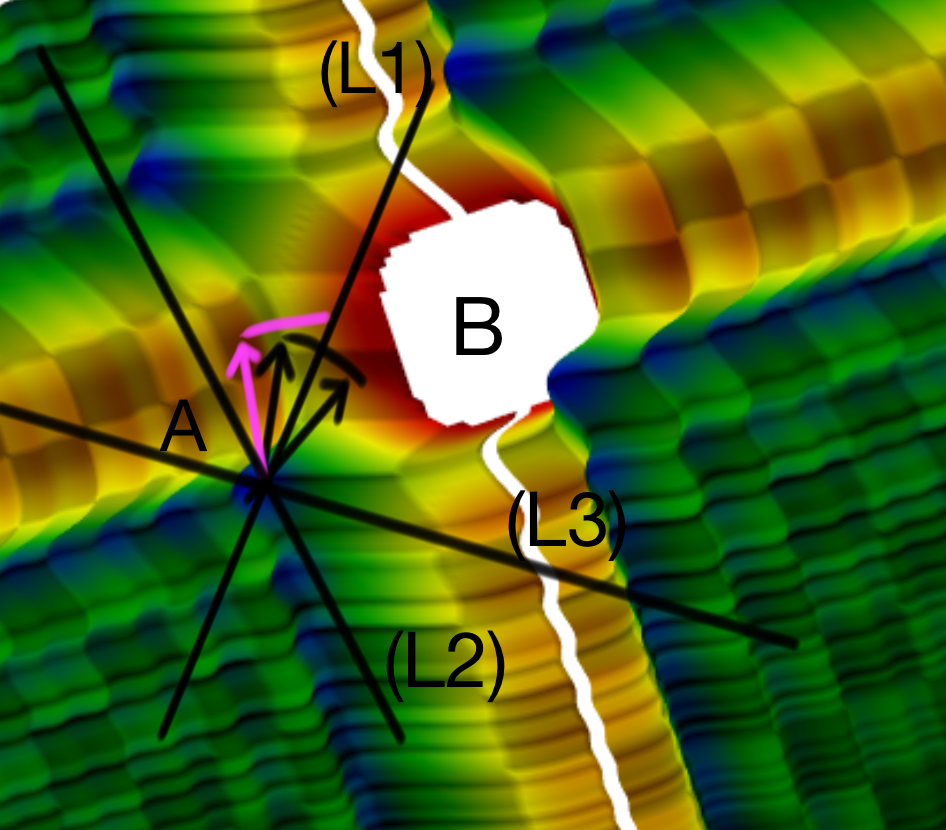
Could a gradient aggregation rule (GAR) for distributed machine learning be both robust and fast? This paper answers by the affirmative through multi-Bulyan. Given $n$ workers, $f$ of which are arbitrary malicious (Byzantine) and $m=n-f$ are not, we prove that multi-Bulyan can ensure a strong form of Byzantine resilience, as well as an ${\frac{m}{n}}$ slowdown, compared to averaging, the fastest (but non Byzantine resilient) rule for distributed machine learning. When $m \approx n$ (almost all workers are correct), multi-Bulyan reaches the speed of averaging. We also prove that multi-Bulyan's cost in local computation is $O(d)$ (like averaging), an important feature for ML where $d$ commonly reaches $10^9$, while robust alternatives have at least quadratic cost in $d$. Our theoretical findings are complemented with an experimental evaluation which, in addition to supporting the linear $O(d)$ complexity argument, conveys the fact that multi-Bulyan's parallelisability further adds to its efficiency.
翻译:分布式机器学习的梯度汇总规则( GAR) 能否既有力又快速? 本文通过多布林语的肯定回答是肯定的。 鉴于美元工人,其中美元是任意恶意( Byzantine) 和 美元=n- f$不是,我们证明多布林可以确保强大的Byzantine抗御能力形式,以及美元(frac{m ⁇ n ⁇ $)的减速,与平均相比,这是分布式机器学习最快(但非Byzantine有弹性)的规则。当美元(几乎所有工人都是正确的)时,多布林语达到平均速度。 我们还证明,多布林语在当地计算中的成本是$(d) (类似于平均) 美元,这是多布林语中的一个重要特征,因为美元通常达到 10 ⁇ 9美元,而稳健的替代品至少以美元计算成四分价成本。 我们的理论结论得到了实验性评估的补充,除了支持线性美元(d) 复杂性论证外,还表明多布林的平行性能进一步增加其平行性。