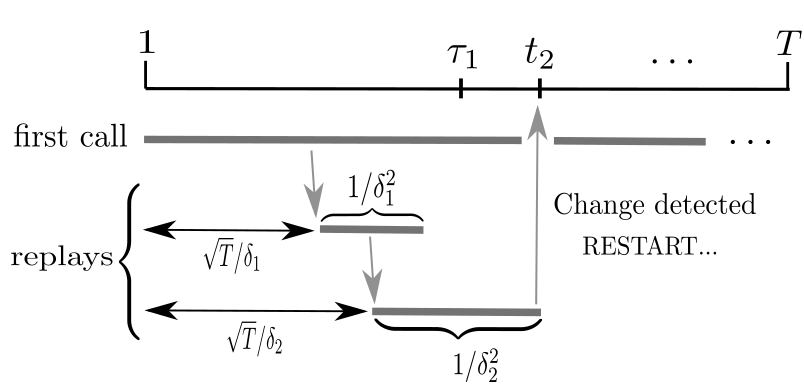
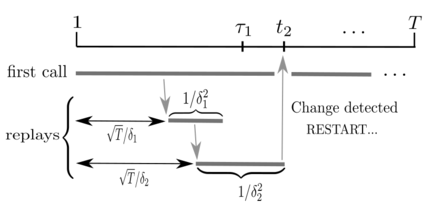
In bandit with distribution shifts, one aims to automatically adapt to unknown changes in reward distribution, and restart exploration when necessary. While this problem has been studied for many years, a recent breakthrough of Auer et al. (2018, 2019) provides the first adaptive procedure to guarantee an optimal (dynamic) regret $\sqrt{LT}$, for $T$ rounds, and an unknown number $L$ of changes. However, while this rate is tight in the worst case, it remained open whether faster rates are possible, without prior knowledge, if few changes in distribution are actually severe. To resolve this question, we propose a new notion of significant shift, which only counts very severe changes that clearly necessitate a restart: roughly, these are changes involving not only best arm switches, but also involving large aggregate differences in reward overtime. Thus, our resulting procedure adaptively achieves rates always faster (sometimes significantly) than $O(\sqrt{ST})$, where $S\ll L$ only counts best arm switches, while at the same time, always faster than the optimal $O(V^{\frac{1}{3}}T^{\frac{2}{3}})$ when expressed in terms of total variation $V$ (which aggregates differences overtime). Our results are expressed in enough generality to also capture non-stochastic adversarial settings.
翻译:虽然这个问题已经研究多年,但最近Auer等人(2018年,2019年)的突破提供了第一个适应性程序,可以保证最优(动力)遗憾$@sqrt{LT}美元($T$)和变化的金额($O(sqrt{LT}),尽管在最坏的情况下,这一利率比较紧,但是,如果分配的变动实际上很少发生严重,那么在不事先知道的情况下,能否实现更快的费率,以及必要时重新开始勘探。为了解决这个问题,我们提出了一个重大转变的新概念,它只计得非常严重的变化,显然需要重新启动:这些变化不仅涉及最好的手臂开关,而且还涉及报酬加班方面的巨大总体差异。因此,我们由此产生的程序所实现的利率总是比美元(sqrt{L}$(sqrt{ST})高($llL$)总是比美元(sllL$)只算最佳的手臂开关,而与此同时,在一般情况下,我们表示的非加班费差异时,总是比美元($=======总差额)。