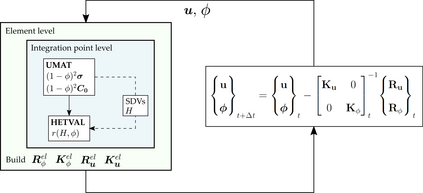
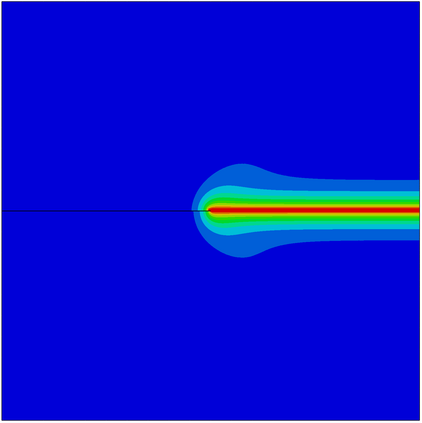
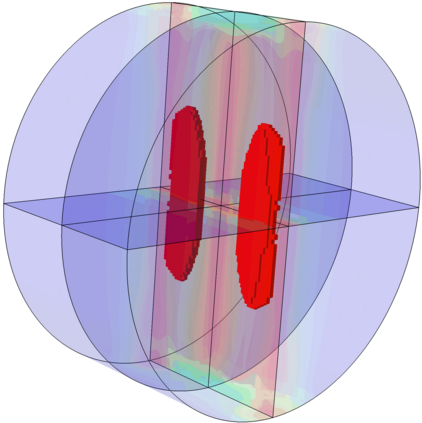
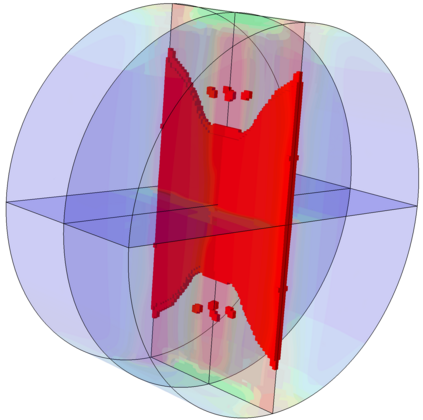
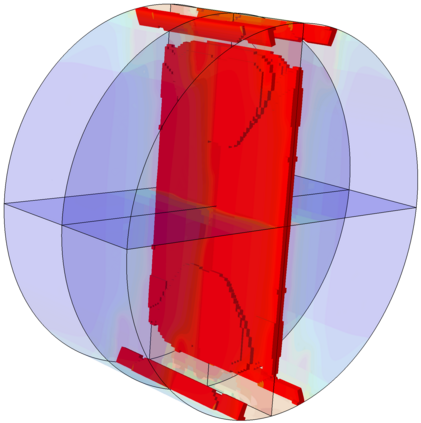
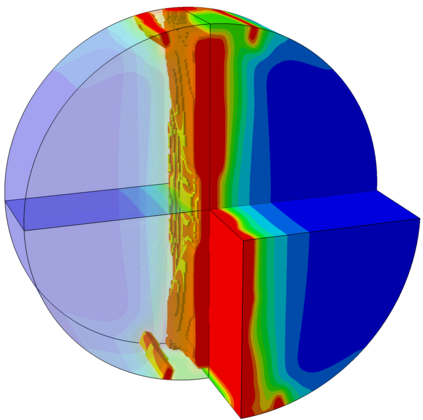
The phase field fracture method is attracting significant interest. Phase field approaches have enabled predicting - on arbitrary geometries and dimensions - complex fracture phenomena such as crack branching, coalescence, deflection and nucleation. In this work, we present a simple and robust implementation of the phase field fracture method in the commercial finite element package Abaqus. The implementation exploits the analogy between the phase field evolution law and the heat transfer equation, enabling the use of Abaqus' in-built features and circumventing the need for defining user elements. The framework is general, and is shown to accommodate different solution schemes (staggered and monolithic), as well as various constitutive choices for preventing damage under compression. The robustness and applicability of the numerical framework presented is demonstrated by addressing several 2D and 3D boundary value problems of particular interest. Focus is on the solution of paradigmatic case studies that are known to be particularly demanding from a convergence perspective. The results reveal that our phase field fracture implementation can be readily combined with other advanced computational features, such as contact, and deliver robust and precise solutions. The code developed can be downloaded from www.empaneda.com/codes.
翻译:相片断裂法正在引起人们的极大兴趣。 相片场断裂法已经使得可以对任意的地貌和方方面面的复杂断裂现象进行预测,如裂缝分枝、联结、偏转和核核裂现象。 在这项工作中,我们展示了商业有限元素包Abaqus 中阶段场断裂法的简单而有力的实施。 实施时利用了阶段场演变法和热传输方程之间的类推,使得能够使用Abaqus的内在特征,并绕过界定用户要素的需要。 该框架是一般性的,并显示它包含不同的解决方案(交错和单片状的),以及防止压缩损害的各种构成选择。 所介绍的数字框架的健全性和适用性表现在解决若干2D和3D特别感兴趣的边界值问题时。 重点是典型案例研究的解决方案,人们从趋同的角度来看特别需要。 其结果显示,我们的场骨折执行可以很容易与其他先进的计算特征(例如接触)结合,并交付稳健和精确的解决方案。 所开发的代码可以从 www.empaneda/com.com) 下载。