Regression via Kirszbraun Extension

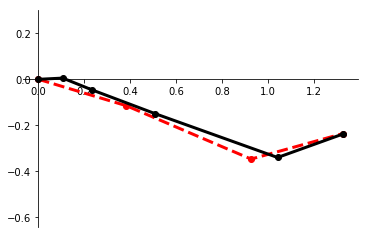
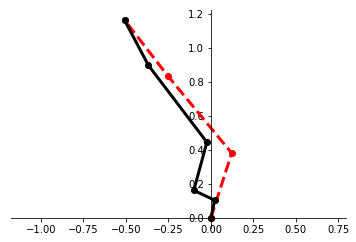
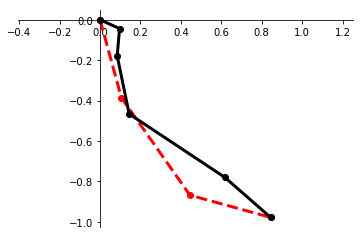
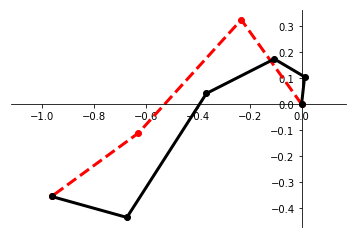
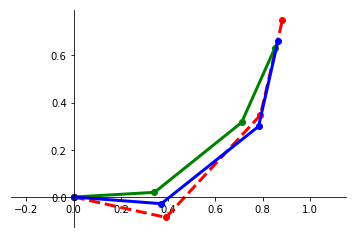
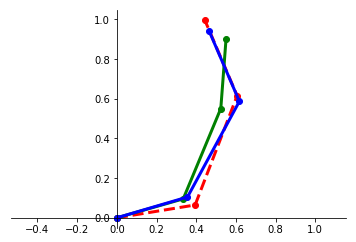
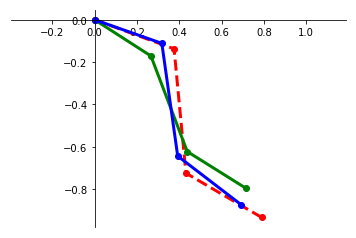
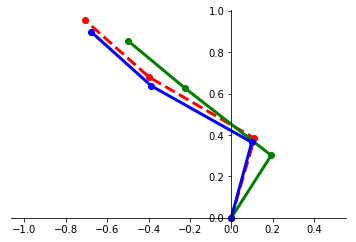
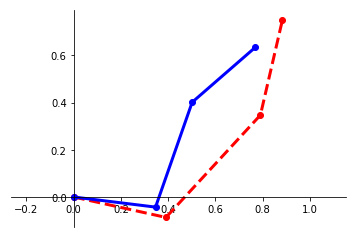
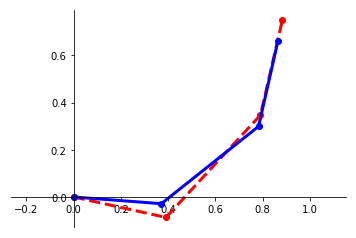
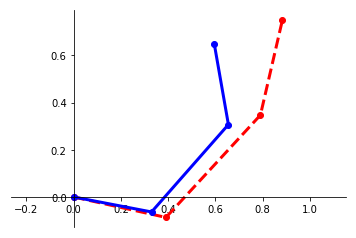
We present a framework for performing regression between two Hilbert spaces. We accomplish this via Kirszbraun's extension theorem -- apparently the first application of this technique to supervised learning -- and analyze its statistical and computational aspects. We begin by formulating the correspondence problem in terms of quadratically constrained quadratic program (QCQP) regression. Then we describe a procedure for smoothing the training data, which amounts to regularizing hypothesis complexity via its Lipschitz constant. The Lipschitz constant is tuned via a Structural Risk Minimization (SRM) procedure, based on the covering-number risk bounds we derive. We apply our technique to learn a transformation between two robotic manipulators with different embodiments, and report promising results.