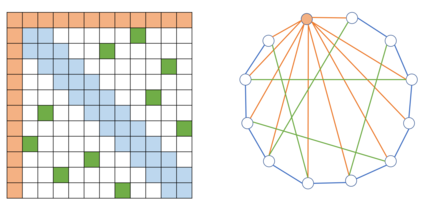
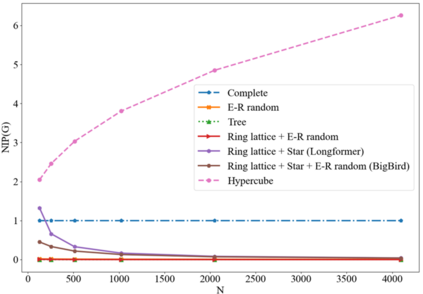
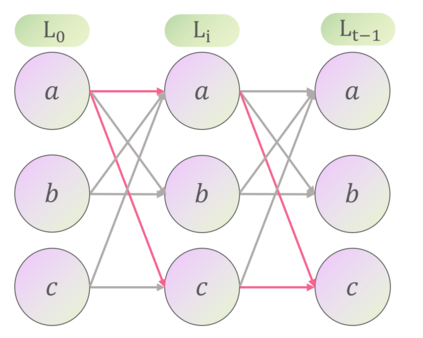
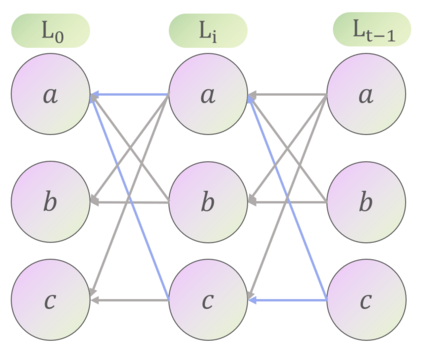
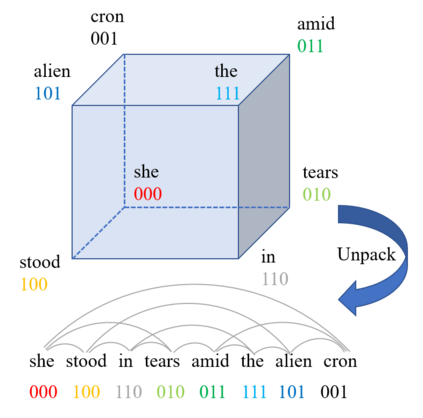
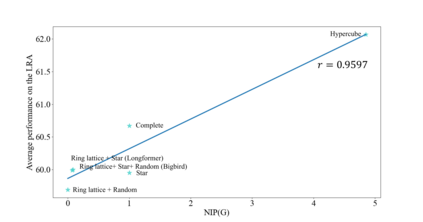
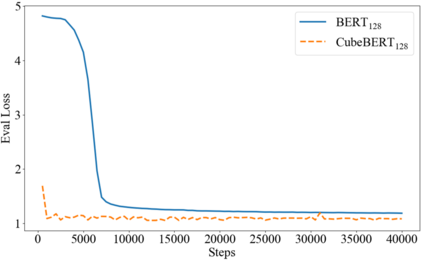
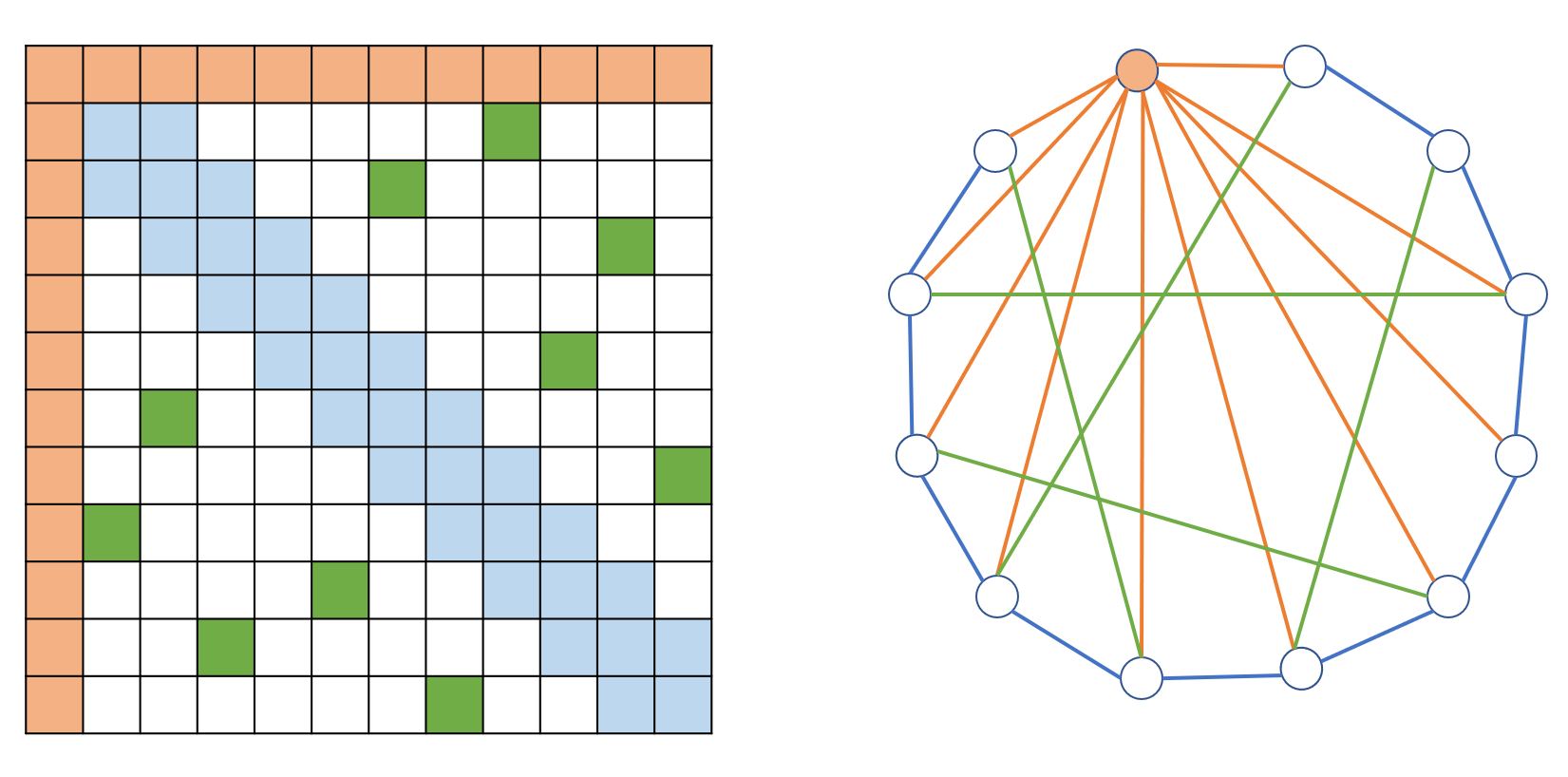
Transformers have made progress in miscellaneous tasks, but suffer from quadratic computational and memory complexities. Recent works propose sparse Transformers with attention on sparse graphs to reduce complexity and remain strong performance. While effective, the crucial parts of how dense a graph needs to be to perform well are not fully explored. In this paper, we propose Normalized Information Payload (NIP), a graph scoring function measuring information transfer on graph, which provides an analysis tool for trade-offs between performance and complexity. Guided by this theoretical analysis, we present Hypercube Transformer, a sparse Transformer that models token interactions in a hypercube and shows comparable or even better results with vanilla Transformer while yielding $O(N\log N)$ complexity with sequence length $N$. Experiments on tasks requiring various sequence lengths lay validation for our graph function well.
翻译:变异器在各种任务中取得了进步,但受到四级计算和记忆复杂性的影响。 最近的工程在稀疏的图表上提出了稀疏的变异器,以降低复杂性并保持强劲的性能。 虽然有效,但是没有充分探讨图需要高密度才能很好地运行的关键部分。 在本文中,我们提出了标准化信息有效载荷(NIP),这是测量图上信息传输的图表评分功能,为业绩和复杂性之间的取舍提供了分析工具。 在这种理论分析的指导下,我们提出了超立方变异器,这是一个稀疏的变异器,在超立方中代表互动,显示与香草变异器的类似或更好的结果,同时产生序列长度为$O(N)$(N)$(N)美元(N)美元(美元)的复杂情况。 有关需要不同序列长度的任务的实验为我们图形功能提供了良好的验证。