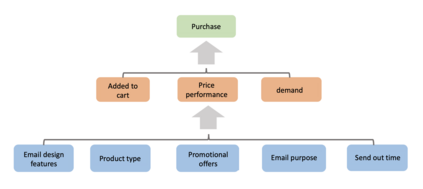
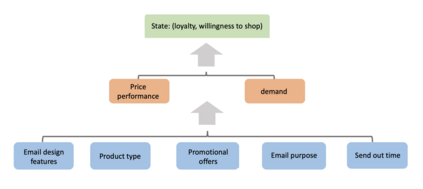
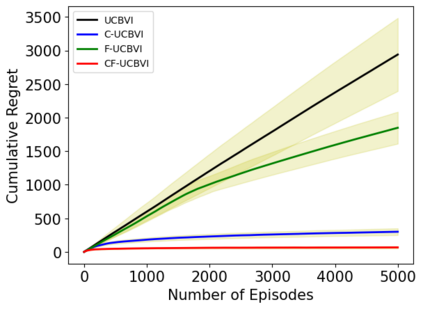
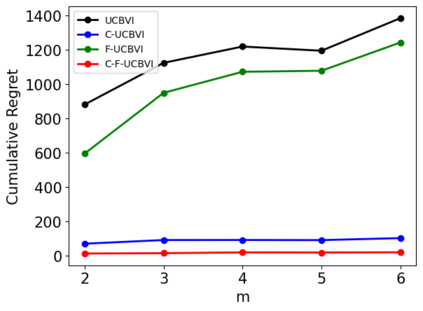
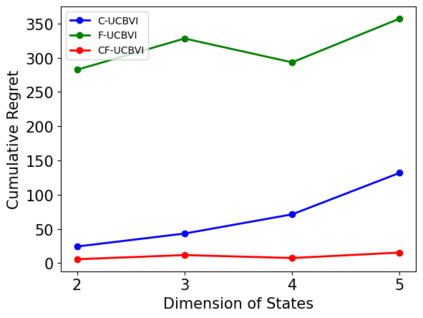
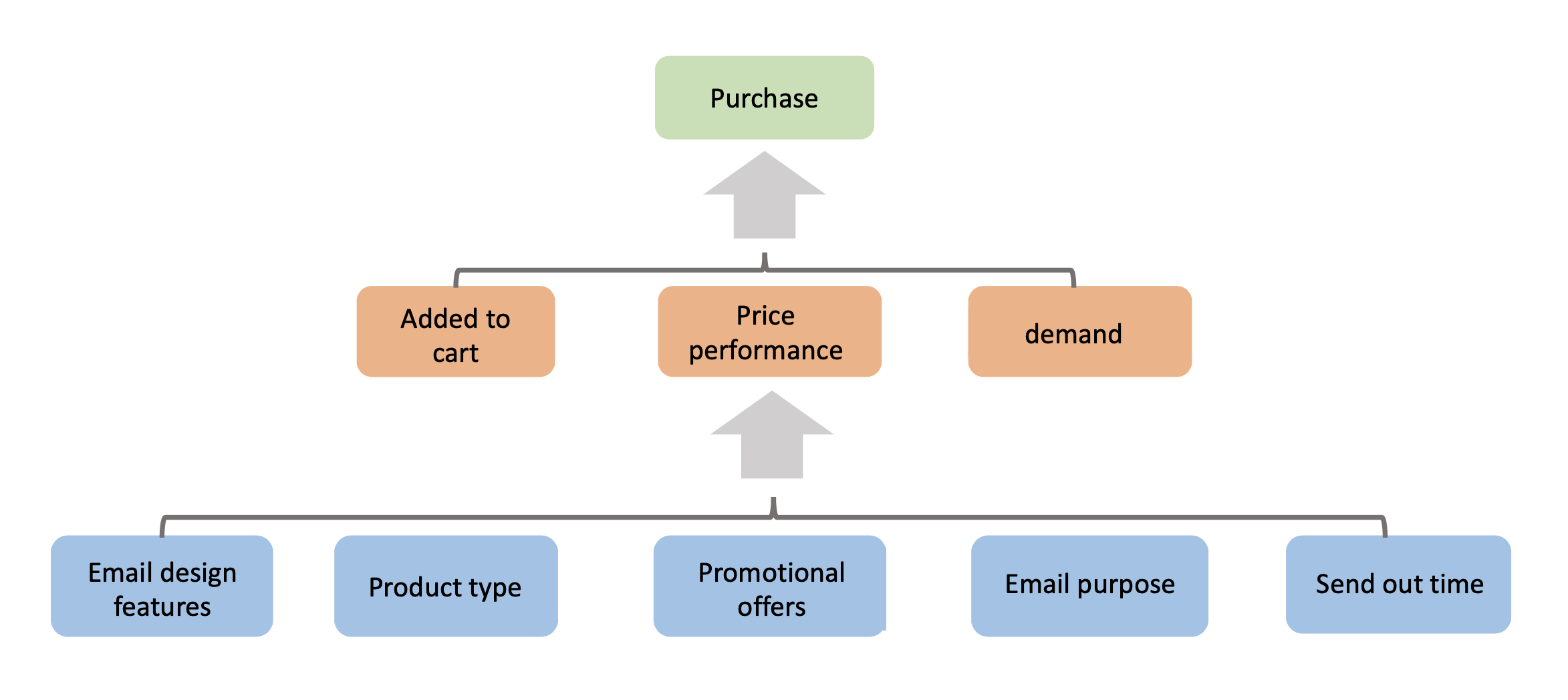
We introduce causal Markov Decision Processes (C-MDPs), a new formalism for sequential decision making which combines the standard MDP formulation with causal structures over state transition and reward functions. Many contemporary and emerging application areas such as digital healthcare and digital marketing can benefit from modeling with C-MDPs due to the causal mechanisms underlying the relationship between interventions and states/rewards. We propose the causal upper confidence bound value iteration (C-UCBVI) algorithm that exploits the causal structure in C-MDPs and improves the performance of standard reinforcement learning algorithms that do not take causal knowledge into account. We prove that C-UCBVI satisfies an $\tilde{O}(HS\sqrt{ZT})$ regret bound, where $T$ is the the total time steps, $H$ is the episodic horizon, and $S$ is the cardinality of the state space. Notably, our regret bound does not scale with the size of actions/interventions ($A$), but only scales with a causal graph dependent quantity $Z$ which can be exponentially smaller than $A$. By extending C-UCBVI to the factored MDP setting, we propose the causal factored UCBVI (CF-UCBVI) algorithm, which further reduces the regret exponentially in terms of $S$. Furthermore, we show that RL algorithms for linear MDP problems can also be incorporated in C-MDPs. We empirically show the benefit of our causal approaches in various settings to validate our algorithms and theoretical results.
翻译:我们引入了因果的Markov决定过程(C-MDPs),这是将标准 MDP的制定与国家过渡和奖励功能的因果结构相结合的顺序决策的新形式主义。许多当代和新兴应用领域,如数字保健和数字营销,可以受益于与C-MDPs建模,因为干预和州/奖励关系背后的因果机制。我们提出了因果的上限信任约束值迭代(C-UCBVI)算法,该算法利用了C-DPs的因果结构,改进了标准强化学习算法的性能,而这种算法没有考虑到因果知识。我们证明C-UCBVI公司满足了美元(HS\sqrt{O})和数字营销等新兴应用领域。由于T$是C-MDPs(H)的总时间步骤,美元是州/回报度之间的因果机制,而美元是国家空间的基点。我们感到遗憾的是,C-DP公司的行动/行动规模(A$)没有缩小,但只有根据因果图表计算出美元,其数值可能指数小于$A$A.