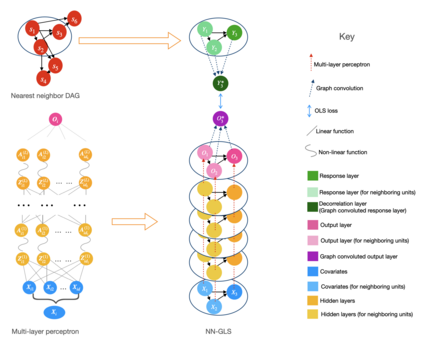
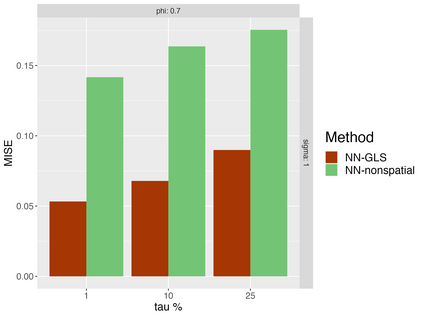
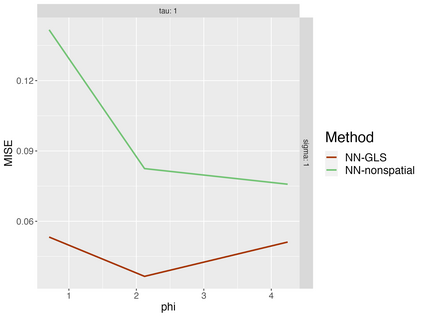
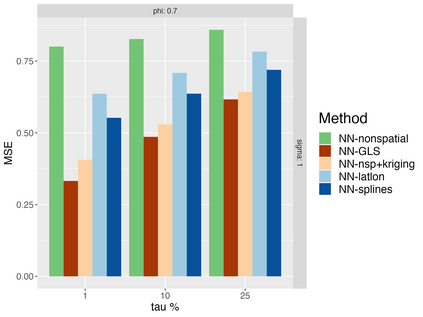
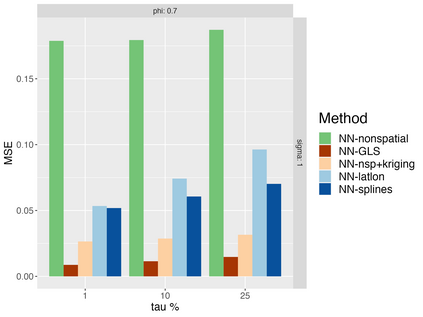
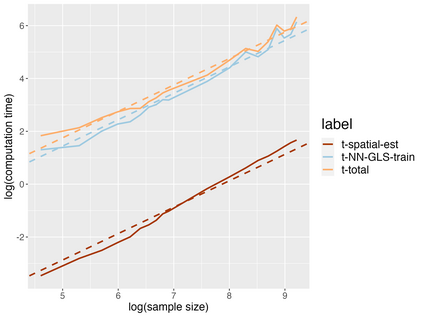
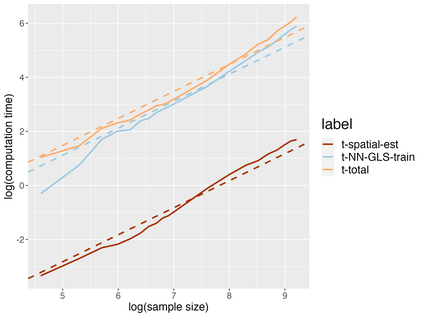
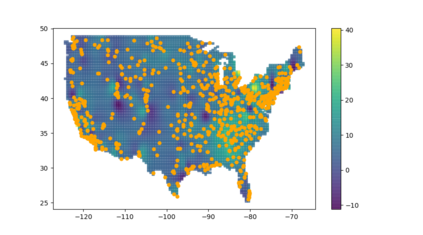
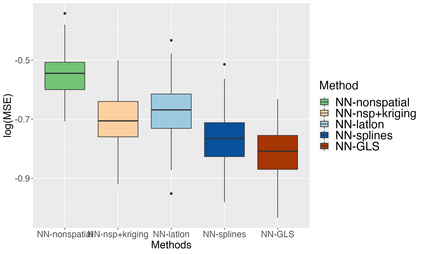
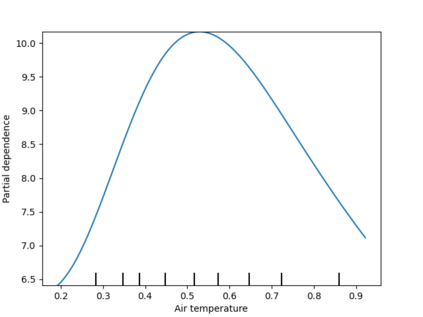
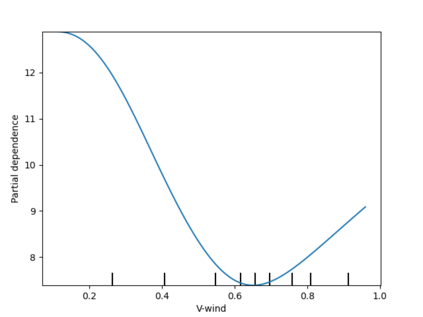
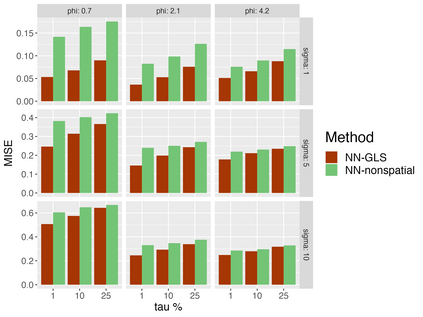
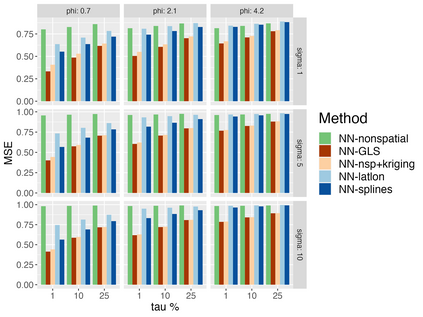
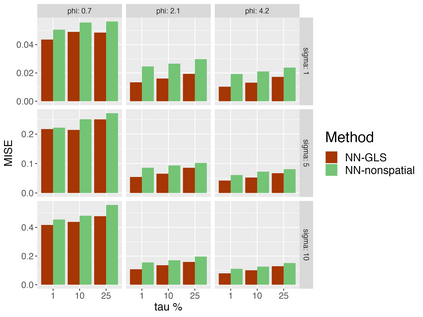
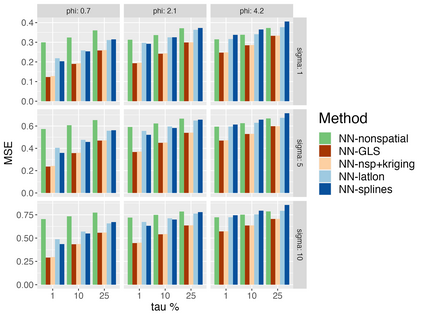
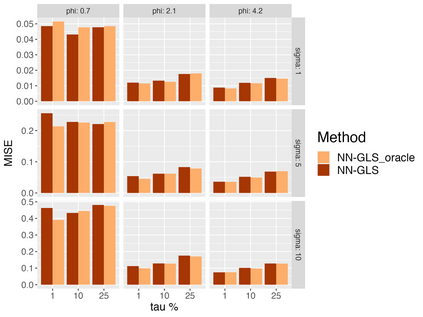
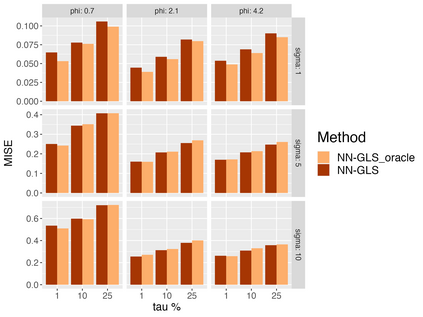
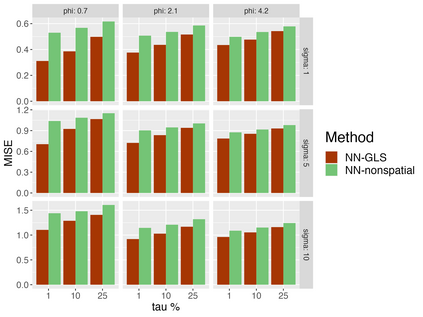
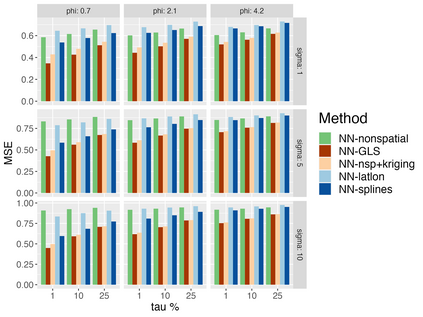
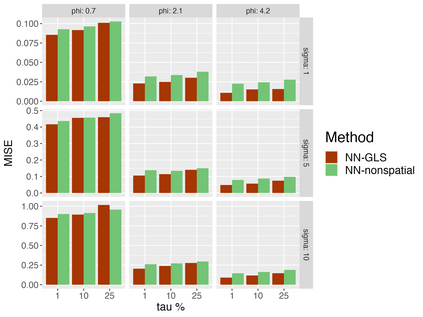
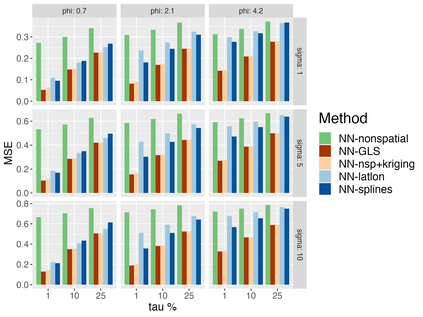
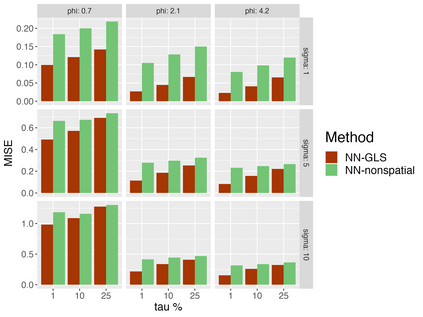
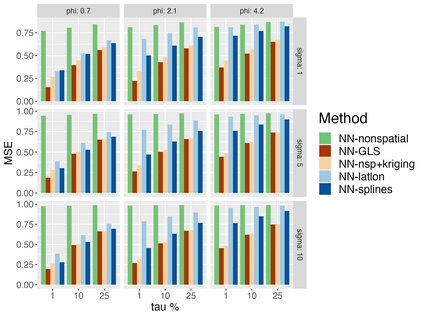
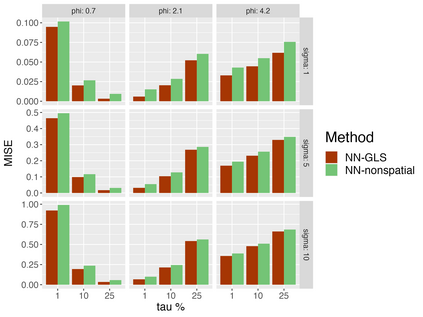
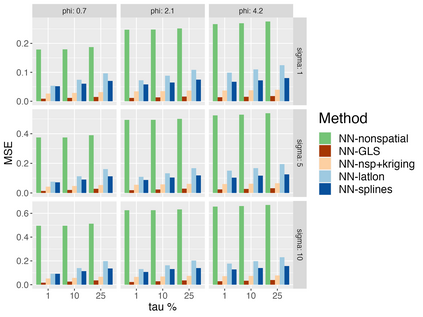
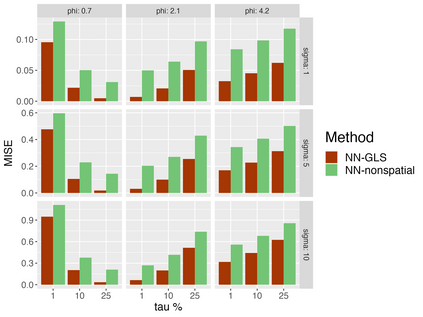
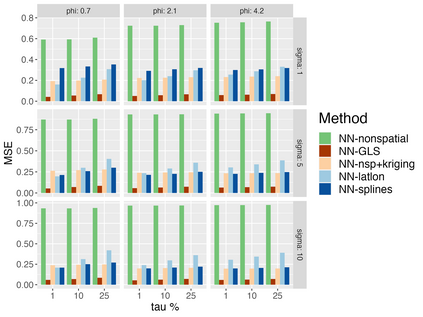
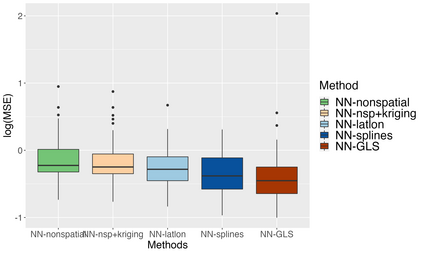
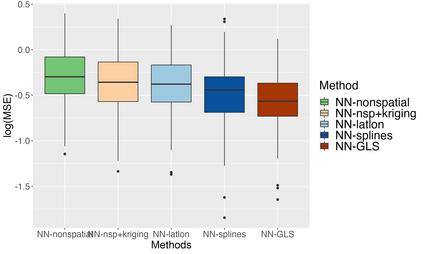
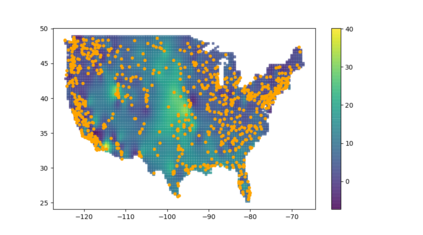
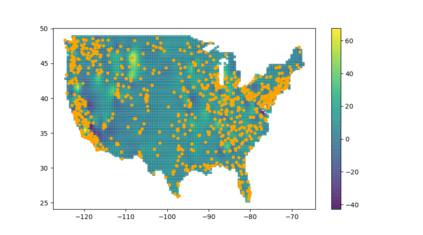
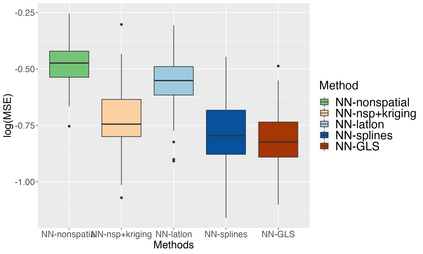
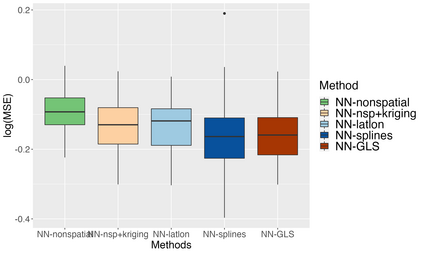
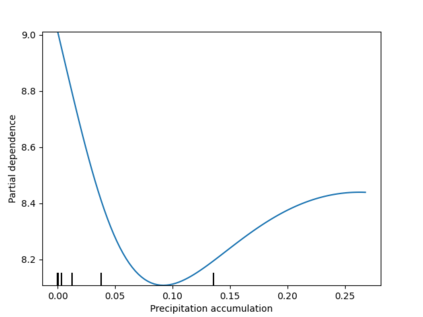
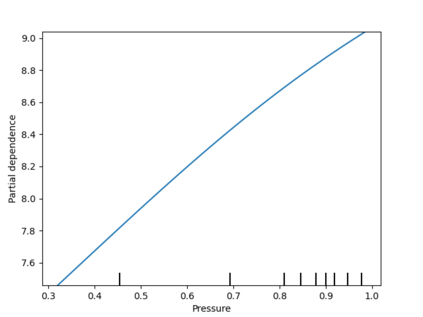
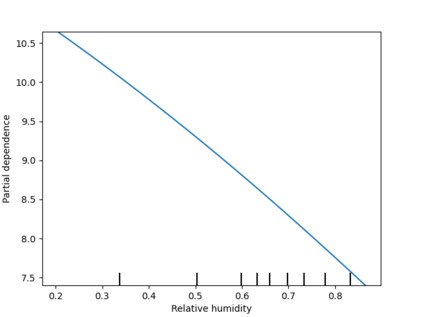
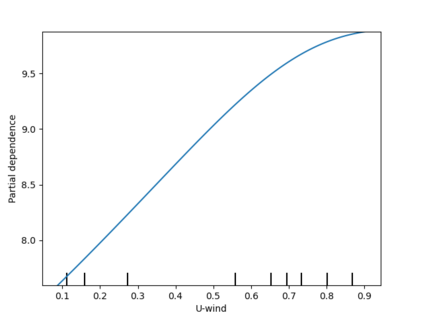
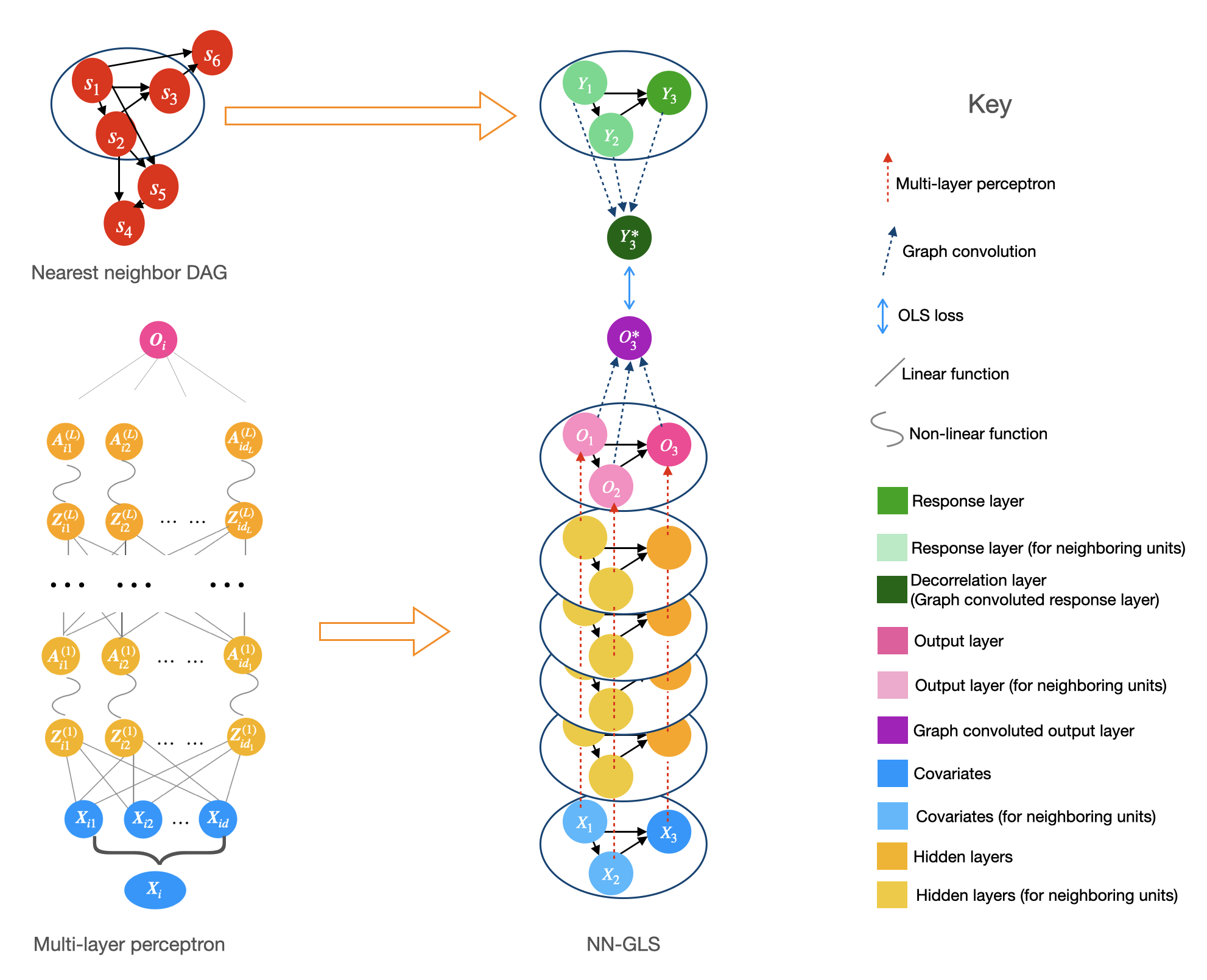
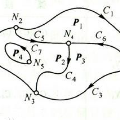
Analysis of geospatial data has traditionally been model-based, with a mean model, customarily specified as a linear regression on the covariates, and a covariance model, encoding the spatial dependence. We relax the strong assumption of linearity and propose embedding neural networks directly within the traditional geostatistical models to accommodate non-linear mean functions while retaining all other advantages including use of Gaussian Processes to explicitly model the spatial covariance, enabling inference on the covariate effect through the mean and on the spatial dependence through the covariance, and offering predictions at new locations via kriging. We propose NN-GLS, a new neural network estimation algorithm for the non-linear mean in GP models that explicitly accounts for the spatial covariance through generalized least squares (GLS), the same loss used in the linear case. We show that NN-GLS admits a representation as a special type of graph neural network (GNN). This connection facilitates use of standard neural network computational techniques for irregular geospatial data, enabling novel and scalable mini-batching, backpropagation, and kriging schemes. Theoretically, we show that NN-GLS will be consistent for irregularly observed spatially correlated data processes. To our knowledge this is the first asymptotic consistency result for any neural network algorithm for spatial data. We demonstrate the methodology through simulated and real datasets.
翻译:传统上,地理空间数据的分析是基于模型的,通常将均值模型指定为协变量上的线性回归,将协方差模型编码为空间依赖性。我们放宽了线性的强假设,并提出将神经网络直接嵌入到传统空间统计模型中,以适应非线性均值函数,同时保留所有其他优势,包括使用高斯过程显式建模空间协方差,通过均值对协变量效应进行推断,并通过协方差对空间依赖性进行推断,通过克里金进行新位置的预测。我们提出了NN-GLS,一种新的神经网络估计算法,用于GP模型中的非线性均值,该算法通过广义最小二乘法(GLS)显式考虑了空间协方差,与线性情况下使用的损失相同。我们证明了NN-GLS具有特殊类型的图神经网络(GNN)表示。这种联系有助于使用标准神经网络计算技术处理不规则地理空间数据,从而实现了新颖和可伸缩的mini-batching、backpropagation和kriging方案。理论上,我们证明了NN-GLS适用于不规则观测的空间相关数据过程。据我们所知,这是第一个适用于空间数据的任何神经网络算法的渐近一致性结果。我们通过模拟和实际数据集展示该方法的应用。