Physics-enhanced deep surrogates for PDEs

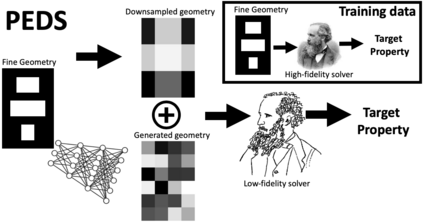
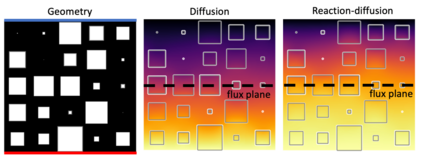
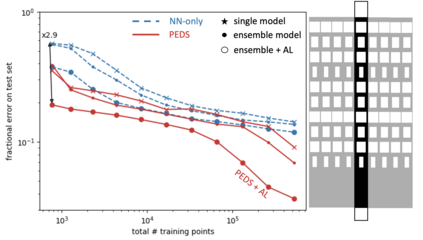
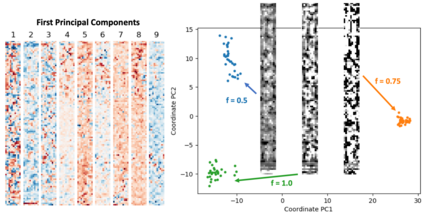
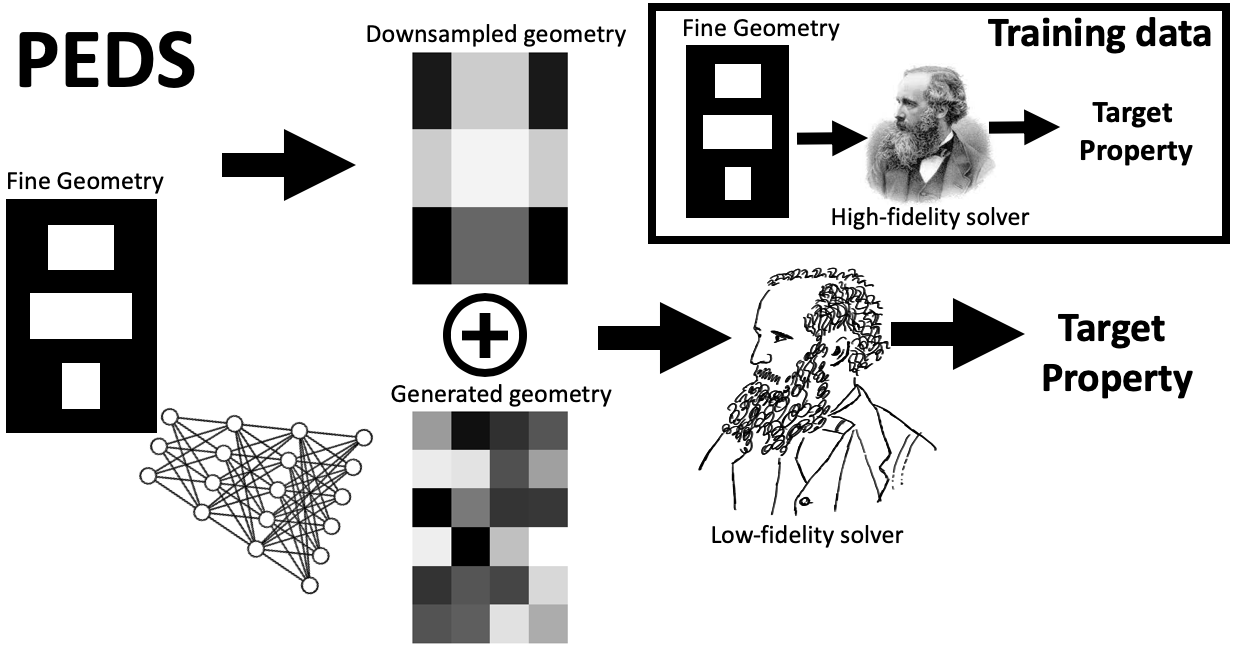
We present a ''physics-enhanced deep-surrogate'' (''PEDS'') approach towards developing fast surrogate models for complex physical systems, which is described by partial differential equations (PDEs) and similar models. Specifically, a unique combination of a low-fidelity, explainable physics simulator and a neural network generator is proposed, which is trained end-to-end to globally match the output of an expensive high-fidelity numerical solver. We consider low-fidelity models derived from coarser discretizations and/or by simplifying the physical equations, which are several orders of magnitude faster than a high-fidelity ''brute-force'' PDE solver. The neural network generates an approximate input, which is adaptively mixed with a downsampled guess and fed into the low-fidelity simulator. In this way, by incorporating the limited physical knowledge from the differentiable low-fidelity model ''layer'', we ensure that the conservation laws and symmetries governing the system are respected by the design of our hybrid system. Experiments on three test problems -- diffusion, reaction-diffusion, and electromagnetic scattering models -- show that a PEDS surrogate can be up to 3$\times$ more accurate than a ''black-box'' neural network with limited data ($\approx 10^3$ training points), and reduces the data needed by at least a factor of 100 for a target error of $5\%$, comparable to fabrication uncertainty. PEDS even appears to learn with a steeper asymptotic power law than black-box surrogates. In summary, PEDS provides a general, data-driven strategy to bridge the gap between a vast array of simplified physical models with corresponding brute-force numerical solvers, offering accuracy, speed, data efficiency, as well as physical insights into the process.