Third-order accurate initialization of VOF volume fractions on unstructured grids with arbitrary polyhedral cells

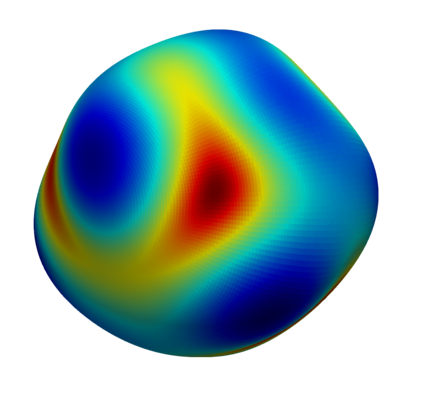
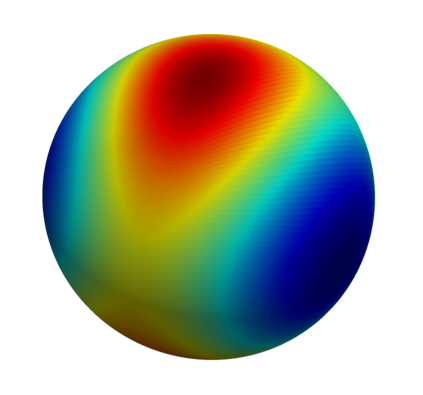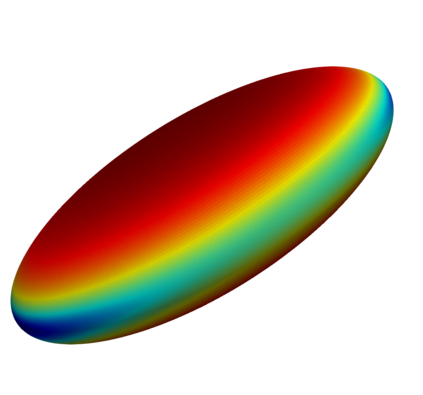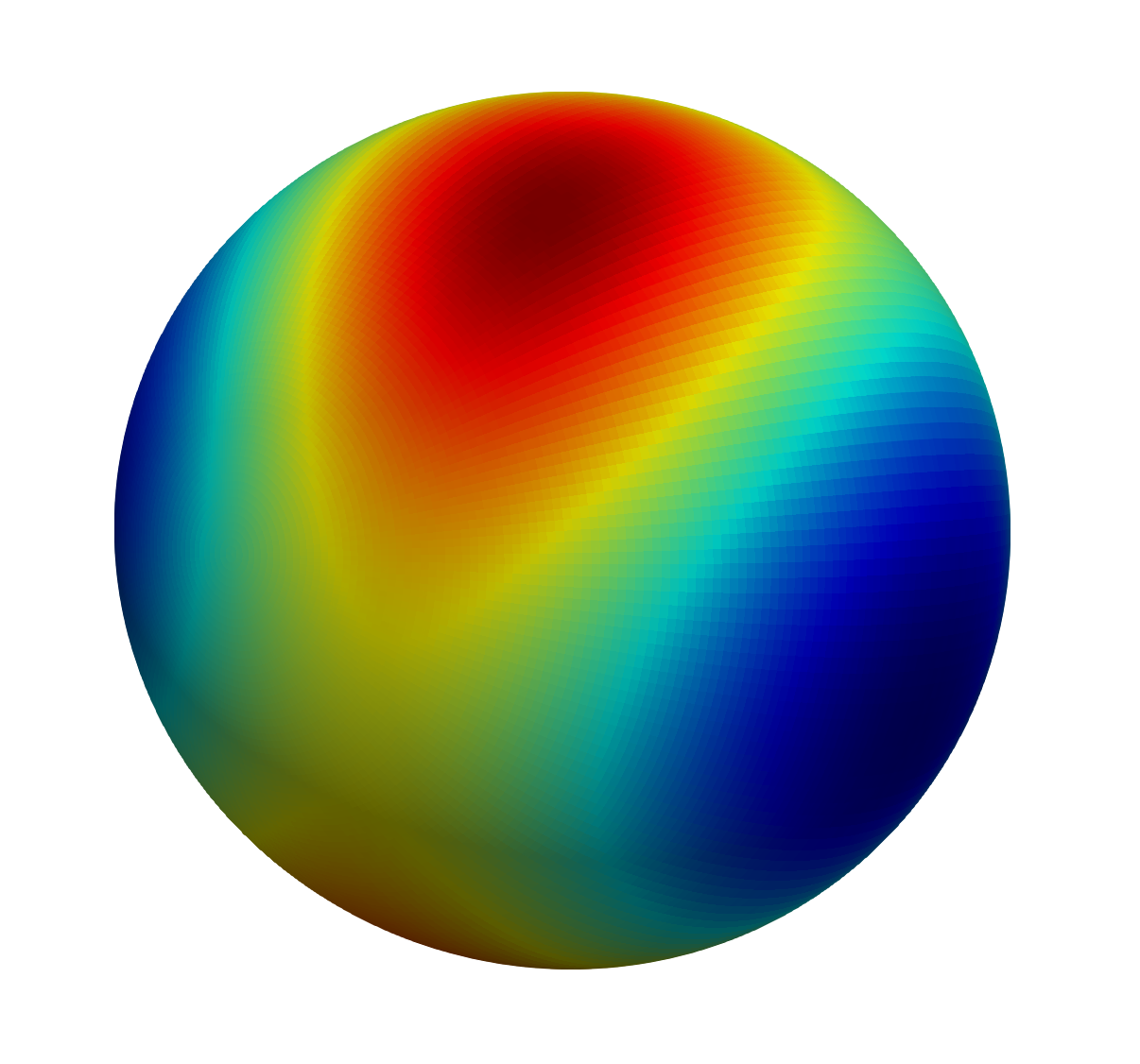This paper introduces a novel method for the efficient and accurate computation of volume fractions on unstructured polyhedral meshes, where the phase boundary is an orientable hypersurface, implicitly given as the iso-contour of a sufficiently smooth level-set function. Locally, i.e.~in each mesh cell, we compute a principal coordinate system in which the hypersurface can be approximated as the graph of an osculating paraboloid. A recursive application of the \textsc{Gaussian} divergence theorem then allows to analytically transform the volume integrals to curve integrals associated to the polyhedron faces, which can be easily approximated numerically by means of standard \textsc{Gauss-Legendre} quadrature. This face-based formulation enables the applicability to unstructured meshes and considerably simplifies the numerical procedure for applications in three spatial dimensions. We discuss the theoretical foundations and provide details of the numerical algorithm. Finally, we present numerical results for convex and non-convex hypersurfaces embedded in cuboidal and tetrahedral meshes, showing both high accuracy and third- to fourth-order convergence with spatial resolution.