Clustering parametric models and normally distributed data

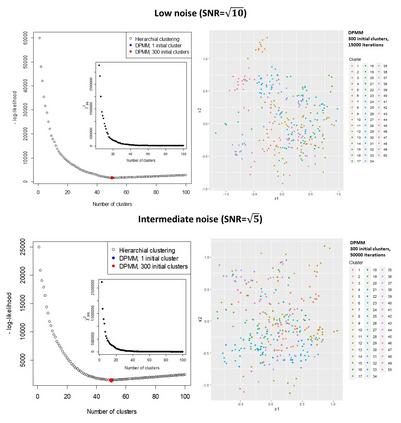
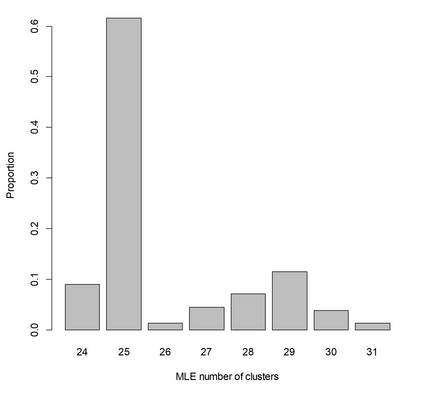
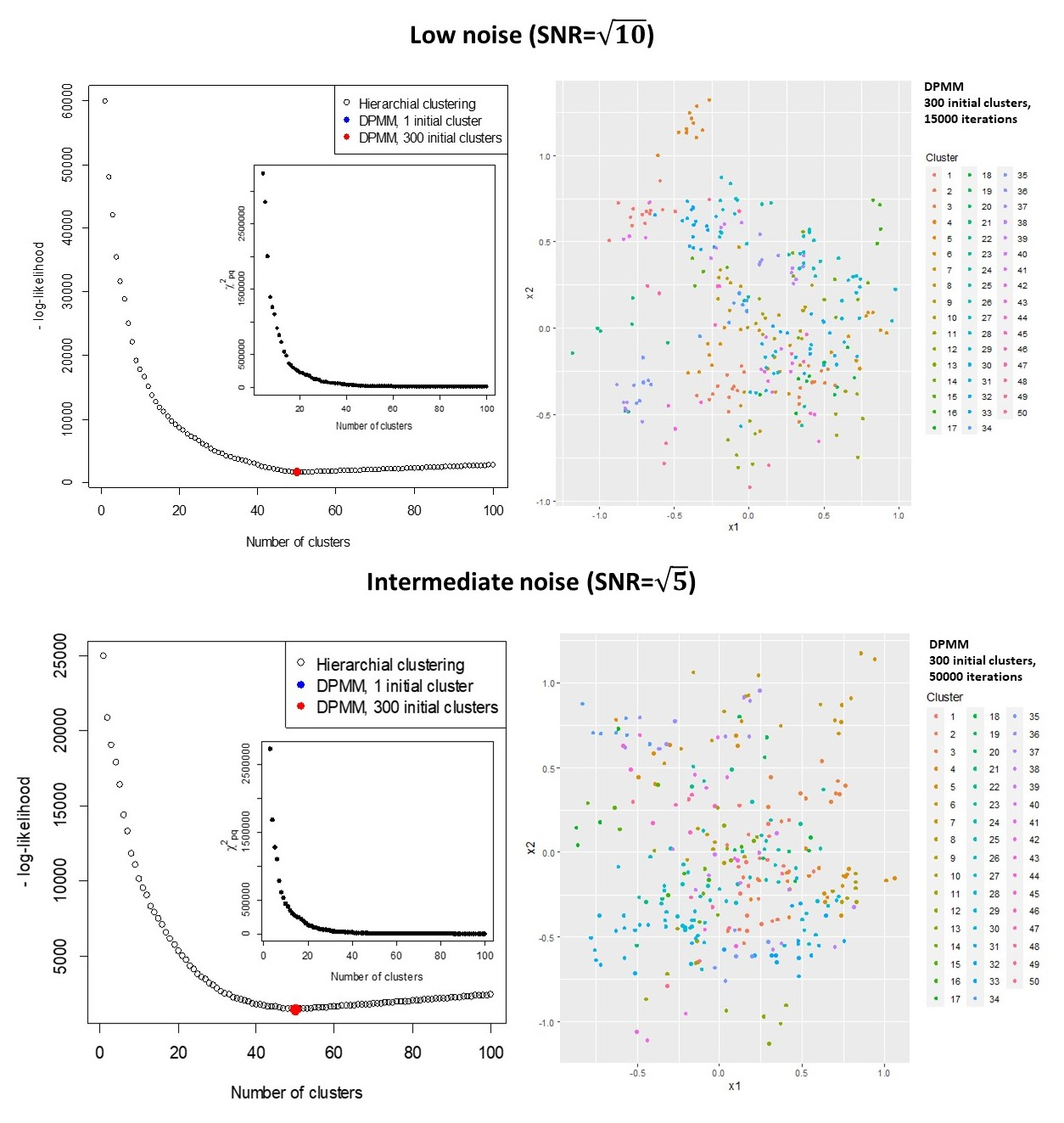
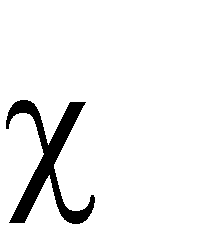A recent UK Biobank study clustered 156 parameterised models associating risk factors with common diseases, to identify shared causes of disease. Parametric models are often more familiar and interpretable than clustered data, can build-in prior knowledge, adjust for known confounders, and use marginalisation to emphasise parameters of interest. Estimates include a Maximum Likelihood Estimate (MLE) that is (approximately) normally distributed, and its covariance. Clustering models rarely consider the covariances of data points, that are usually unavailable. Here a clustering model is formulated that accounts for covariances of the data, and assumes that all MLEs in a cluster are the same. The log-likelihood is exactly calculated in terms of the fitted parameters, with the unknown cluster means removed by marginalisation. The procedure is equivalent to calculating the Bayesian Information Criterion (BIC) without approximation, and can be used to assess the optimum number of clusters for a given clustering algorithm. The log-likelihood has terms to penalise poor fits and model complexity, and can be maximised to determine the number and composition of clusters. Results can be similar to using the ad-hoc "elbow criterion", but are less subjective. The model is also formulated as a Dirichlet process mixture model (DPMM). The overall approach is equivalent to a multi-layer algorithm that characterises features through the normally distributed MLEs of a fitted model, and then clusters the normal distributions. Examples include simulated data, and clustering of diseases in UK Biobank data using estimated associations with risk factors. The results can be applied directly to measured data and their estimated covariances, to the output from clustering models, or the DPMM implementation can be used to cluster fitted models directly.