Staggered schemes for compressible flow: a general construction

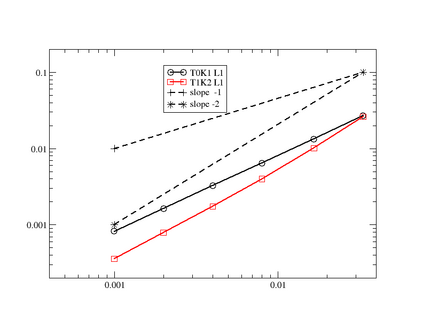
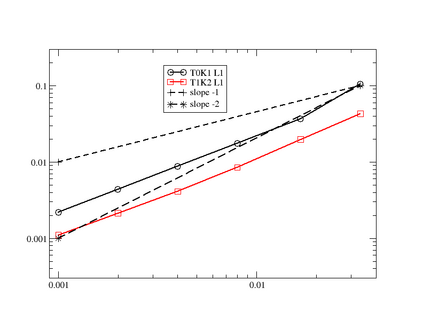
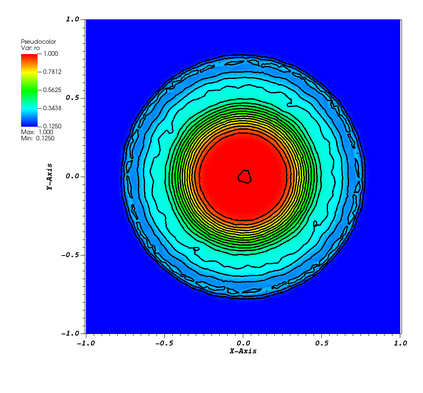
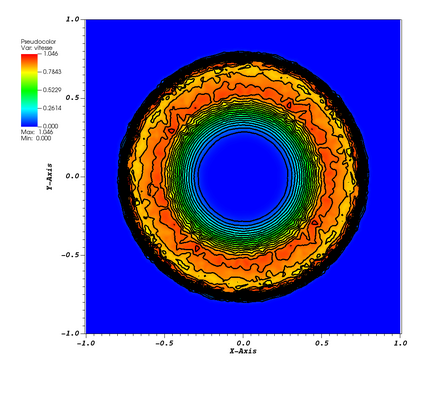
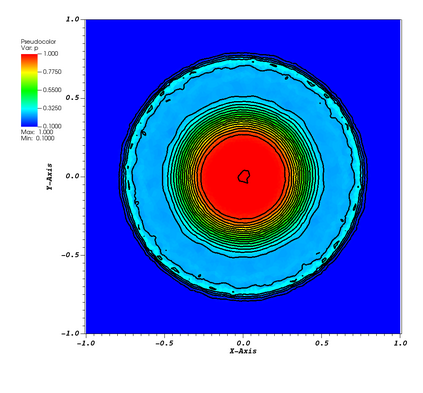
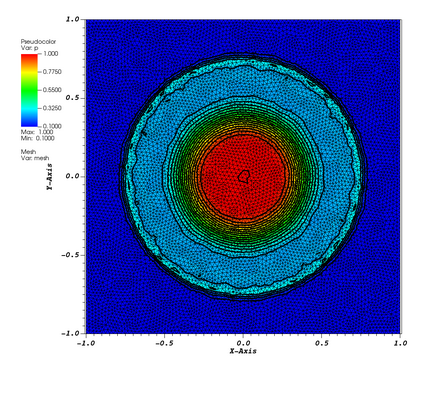
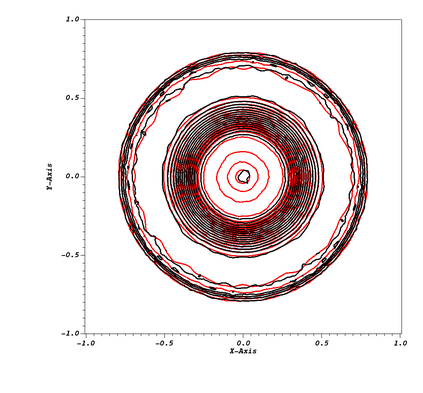
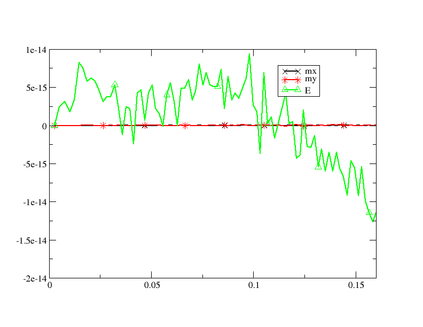
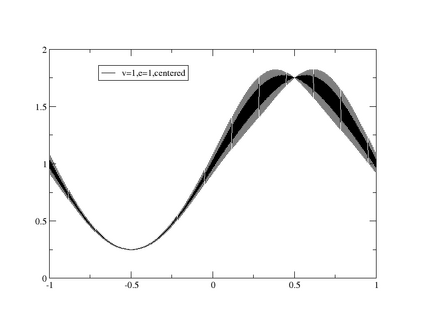
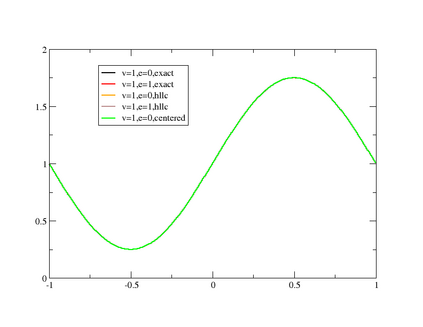
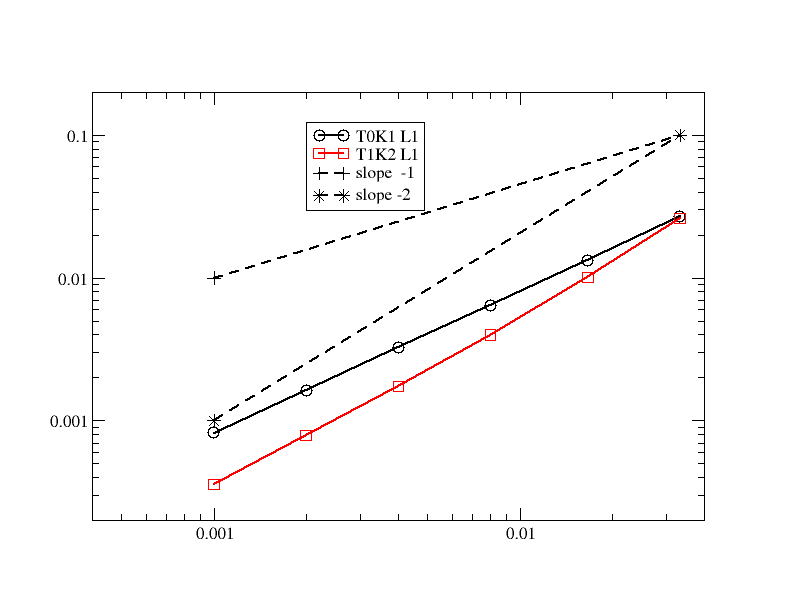
This paper is focused on the approximation of the Euler equations of compressible fluid dynamics on a staggered mesh. With this aim, the flow parameters are described by the velocity, the density and the internal energy. The thermodynamic quantities are described on the elements of the mesh, and thus the approximation is only in $L^2$, while the kinematic quantities are globally continuous. The method is general in the sense that the thermodynamic and kinetic parameters are described by an arbitrary degree of polynomials. In practice, the difference between the degrees of the kinematic parameters and the thermodynamic ones {is set} to $1$. The integration in time is done using the forward Euler method but can be extended straightforwardly to higher-order methods. In order to guarantee that the limit solution will be a weak solution of the problem, we introduce a general correction method in the spirit of the Lagrangian staggered method described in \cite{Svetlana,MR4059382, MR3023731}, and we prove a Lax Wendroff theorem. The proof is valid for multidimensional versions of the scheme, even though most of the numerical illustrations in this work, on classical benchmark problems, are one-dimensional because we have easy access to the exact solution for comparison. We conclude by explaining that the method is general and can be used in different settings, for example, Finite Volume, or discontinuous Galerkin method, not just the specific one presented in this paper.