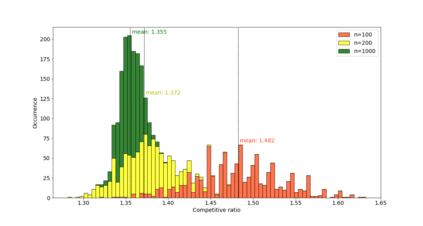
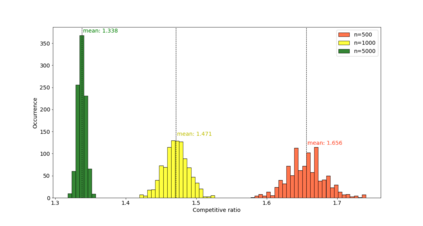
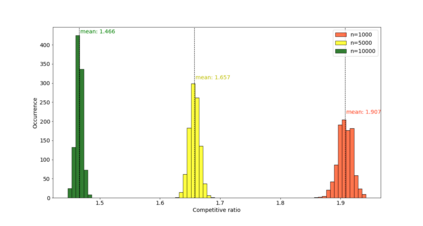
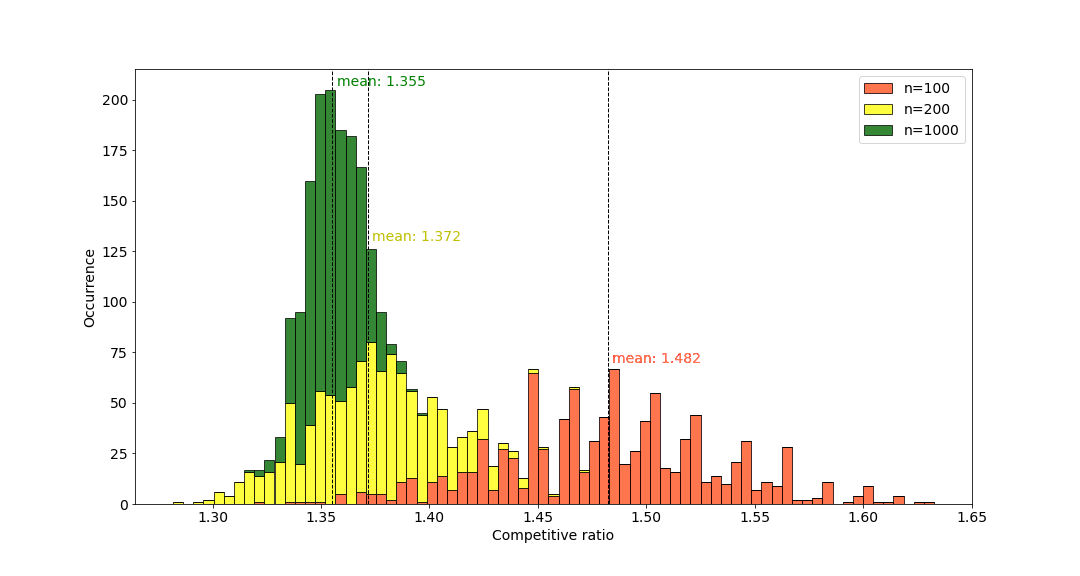
This paper considers a combination of the joint replenishment problem with single machine scheduling. There is a single resource, which is required by all the jobs, and a job can be started at time point $t$ on the machine if and only the machine does not process another job at $t$, and the resource is replenished between its release date and $t$. Each replenishment has a cost, which is independent of the amount replenished. The objective is to minimize the total replenishment cost plus the maximum flow time of the jobs. We consider the online variant of the problem, where the jobs are released over time, and once a job is inserted into the schedule, its starting time cannot be changed. We propose a deterministic 2-competitive online algorithm for the general input. Moreover, we show that for a certain class of inputs (so-called $p$-bounded input), the competitive ratio of the algorithm tends to $\sqrt{2}$ as the number of jobs tends to infinity. We also derive several lower bounds for the best competitive ratio of any deterministic online algorithm under various assumptions.
翻译:本文将联合补充问题与单一机器的日程安排结合起来考虑。 所有工作都需要有一个单一的资源, 并且只要机器不以美元处理另一工作, 就可以在时间点在机器上开始工作, 只要机器不以美元处理另一工作, 并且资源在发行日期和美元之间得到补充。 每一次补充都有成本, 这与补充的数量无关。 目标是将总补充成本和工作的最大流动时间降到最低。 我们考虑的是问题的在线变量, 即工作会随着时间推移而释放, 一旦工作被插入日程, 开始的时间是无法改变的。 我们建议对一般投入采用一种具有确定性的 2 竞争性的在线算法。 此外, 我们表明, 对于某类投入( 所谓的美元约束投入), 算法的竞争性比率往往为 $sqrt{2}, 因为工作的数量往往不尽相同。 我们还在各种假设下为任何确定性在线算法的最佳竞争性比率得出了几个较低的界限。