Data-Driven Optimal Sensor Placement for High-Dimensional System Using Annealing Machine

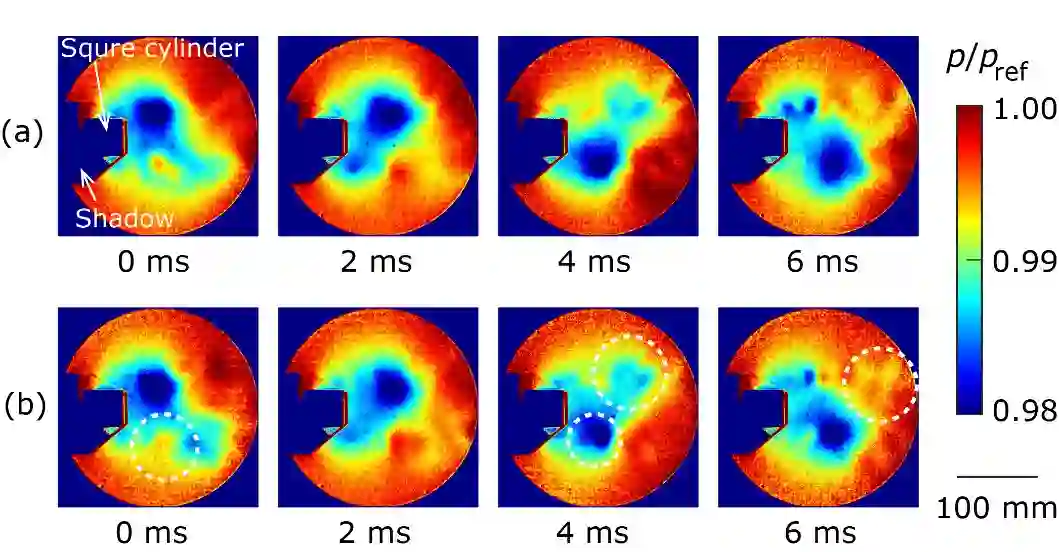
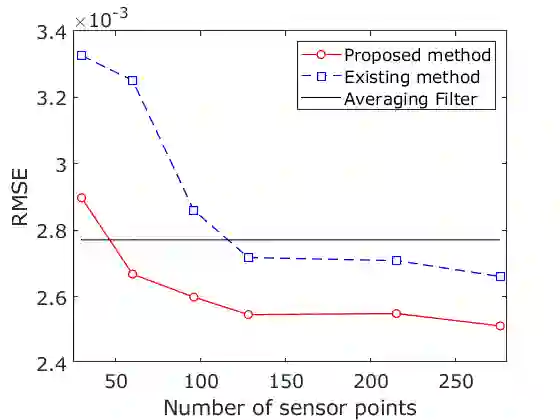
We propose a novel method for solving optimal sensor placement problem for high-dimensional system using an annealing machine. The sensor points are calculated as a maximum clique problem of the graph, the edge weight of which is determined by the proper orthogonal decomposition (POD) mode obtained from data based on the fact that a high-dimensional system usually has a low-dimensional representation. Since the maximum clique problem is equivalent to the independent set problem of the complement graph, the independent set problem is solved using Fujitsu Digital Annealer. As a demonstration of the proposed method, the pressure distribution induced by the K\'arm\'an vortex street behind a square cylinder is reconstructed based on the pressure data at the calculated sensor points. The pressure distribution is measured by pressure-sensitive paint (PSP) technique, which is an optical flow diagnose method. The root mean square errors (RMSEs) between the pressure measured by pressure transducer and the reconstructed pressures (calculated from the proposed method and an existing greedy method) at the same place are compared. As the result, the similar RMSE is achieved by the proposed method using approximately 1/5 number of sensor points obtained by the existing method. This method is of great importance as a novel approach for optimal sensor placement problem and a new engineering application of an annealing machine.