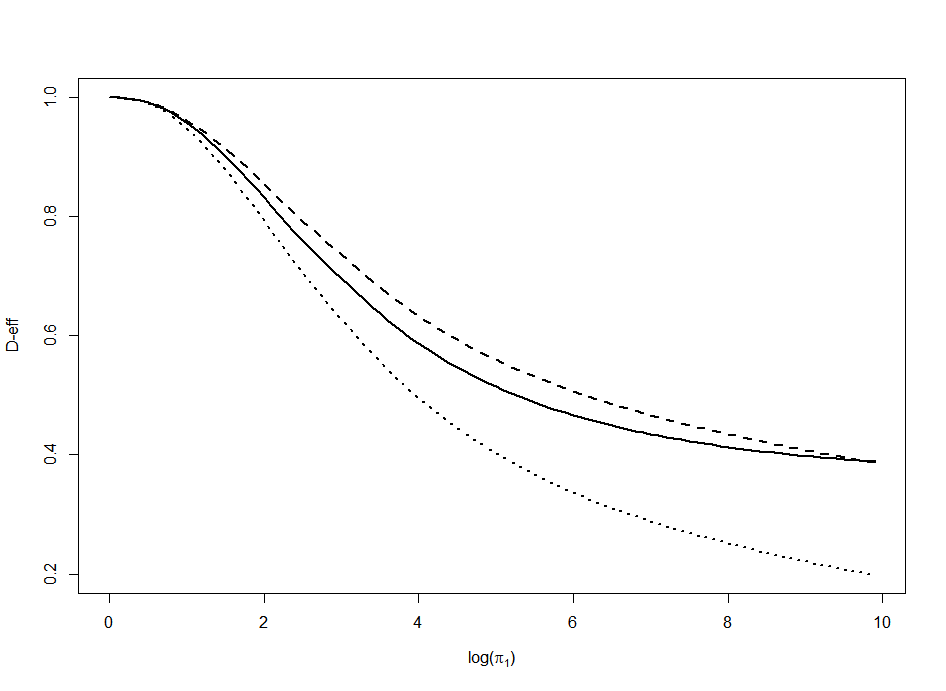
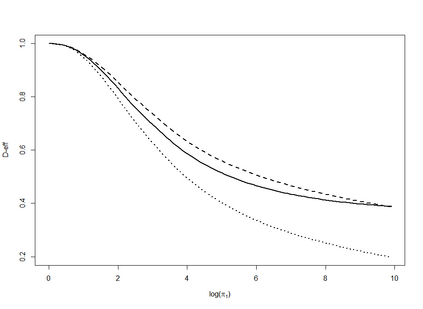
In discrete choice experiments, the information matrix depends on the model parameters. Therefore, $ D $-optimal designs are only locally optimal in the parameter space. This dependence renders the optimization problem very difficult, as standard theory encodes $ D $-optimality in systems of highly nonlinear equations and inequalities. In this work, we connect design theory for discrete choice experiments with Laplacian matrices of connected graphs. We rewrite the $ D $-optimality criterion in terms of Laplacians via Kirchhoff's matrix tree theorem, and show that its dual has a simple description via the Cayley--Menger determinant of the Farris transform of the Laplacian matrix. This results in a drastic reduction of complexity and allows us to implement a gradient descent algorithm to find locally $ D $-optimal designs. For the subclass of Bradley--Terry paired comparison models, we find a direct link to maximum likelihood estimation for Laplacian-constrained Gaussian graphical models. This implies that every locally $ D $-optimal design is a rational function in the parameter when the design is supported on a chordal graph. Finally, we study the performance of our algorithm and demonstrate its application on real and simulated data.
翻译:在离散选择实验中,信息矩阵取决于模型参数。 因此, $ D$- 最佳设计仅在参数空间中是本地最佳的。 这种依赖性使得优化问题非常困难, 因为标准理论将高度非线性方程式和不平等系统中的$ D$- 最佳化编码为高度非线性方程式和不平等。 在这项工作中, 我们将离散选择实验的设计理论与相联图形的Laplacian 矩阵对比模型连接起来。 我们重写了用Kirchhoff 矩阵树的图形模型对 Laplaceans 来说的D$- 最佳性标准, 并显示其双轨通过拉普丽西亚矩阵变法的Cayley- Menger 决定因素简单描述优化问题。 这导致复杂性的大幅降低, 并允许我们使用梯度下降法来查找本地的 $ D $- 最佳化图案设计。 对于布拉德- Termy 配对式比较模型的子类, 我们找到了一个直接链接到 Laplacecian- contragard Gaudes 模型的最大可能性估计。 这意味着, 每一个本地的 $- 都 都 $- 都支持了我们 和 的模型的模型的模型的模型的模型的模型的模拟分析。