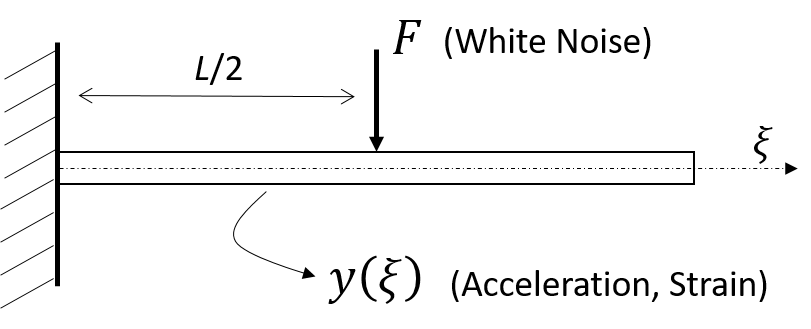
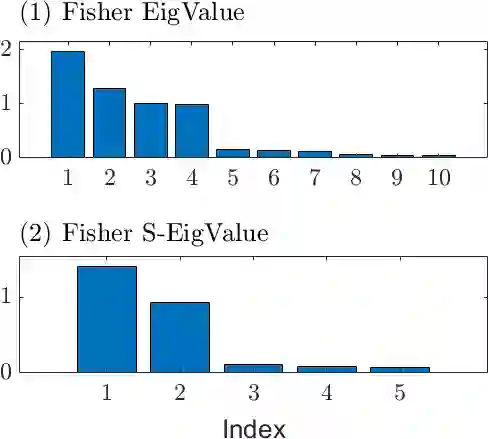
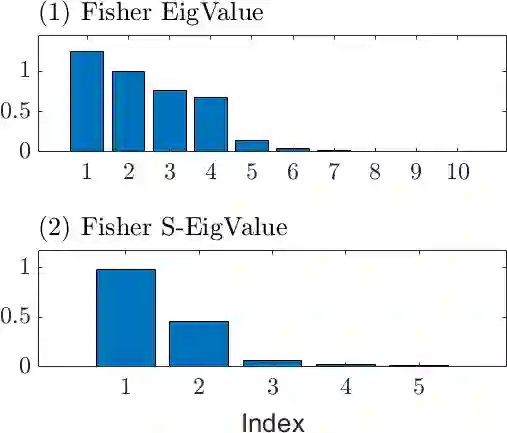
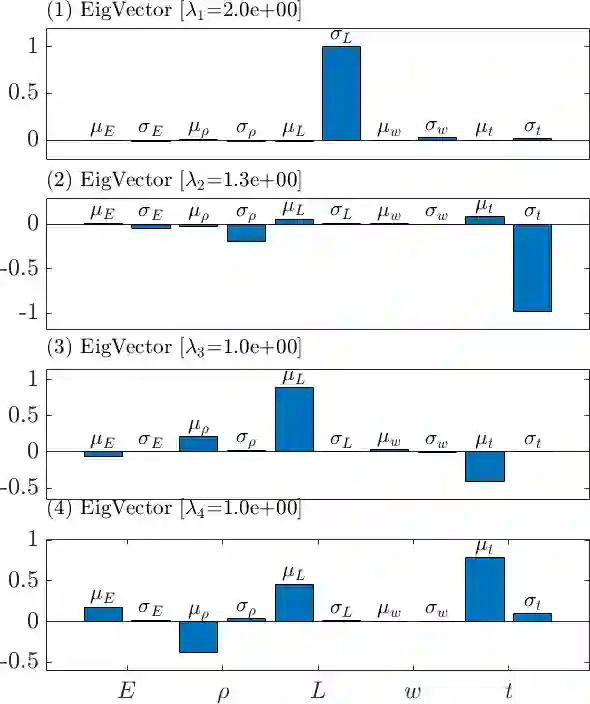
The eigenvalues and eigenvectors of the Fisher information matrix (FIM) can reveal the most and least sensitive directions of a system and it has wide application across science and engineering. We present a symplectic variant of the eigenvalue decomposition for the FIM and extract the sensitivity information with respect to two-parameter conjugate pairs. The symplectic approach decomposes the FIM onto an even-dimensional symplectic basis. This symplectic structure can reveal additional sensitivity information between two-parameter pairs, otherwise concealed in the orthogonal basis from the standard eigenvalue decomposition. The proposed sensitivity approach can be applied to naturally paired two-parameter distribution parameters, or decision-oriented pairing via re-grouping or re-parameterization of the FIM. It can be utilised in tandem with the standard eigenvalue decomposition and offer additional insight into the sensitivity analysis at negligible extra cost.
翻译:渔业信息矩阵(FIM)的成份值和成份能揭示一个系统最最最最最敏感的方向,并且在科学和工程中广泛应用。我们提出了FIM的成份分解的共振变异变体,并提取了两个参数同系配方的敏感信息。共振法将FIM分解成一个平维的共振基础。这种共振结构可以揭示两个参数之间的额外敏感信息,或者在标准电子值分解法的正方形基础上隐藏在两对之间。拟议的敏感度方法可以适用于自然配对的两参数分布参数参数,或者通过FIM的再组合或再校准来进行决策配对。它可以与标准的电子值分解法同步使用,并以微不足道的额外费用对敏感度分析提供额外的洞察力。