Multi-Step Prediction in Linearized Latent State Spaces for Representation Learning

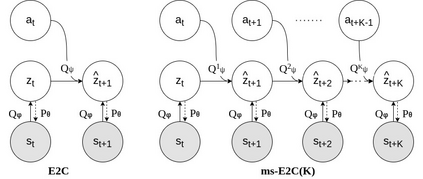
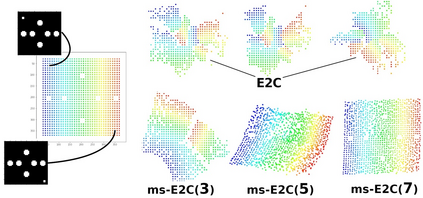
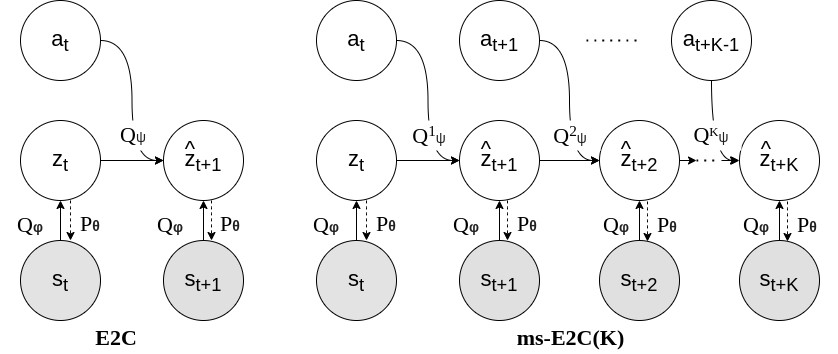
In this paper, we derive a novel method as a generalization over LCEs such as E2C. The method develops the idea of learning a locally linear state space, by adding a multi-step prediction, thus allowing for more explicit control over the curvature. We show, that the method outperforms E2C without drastic model changes which come with other works, such as PCC and P3C. We discuss the relation between E2C and the presented method and derived update equations. We provide empirical evidence, which suggests that by considering the multi-step prediction our method - ms-E2C - allows to learn much better latent state spaces in terms of curvature and next state predictability. Finally, we also discuss certain stability challenges we encounter with multi-step predictions and the ways to mitigate them.