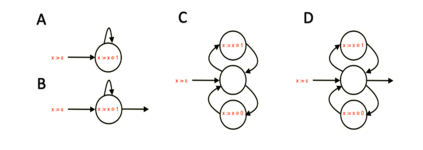
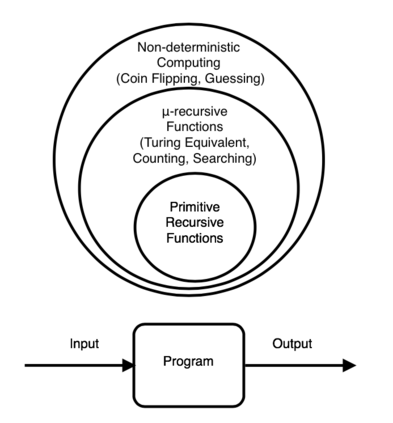
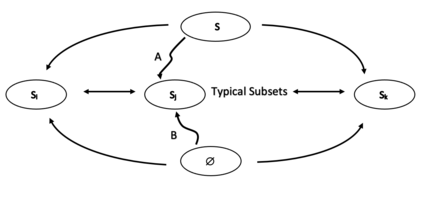
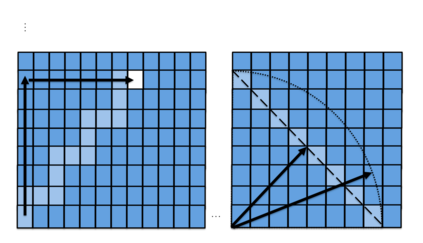
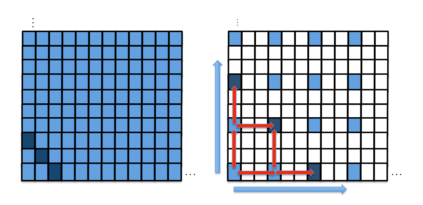
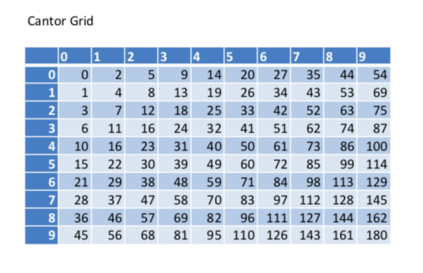
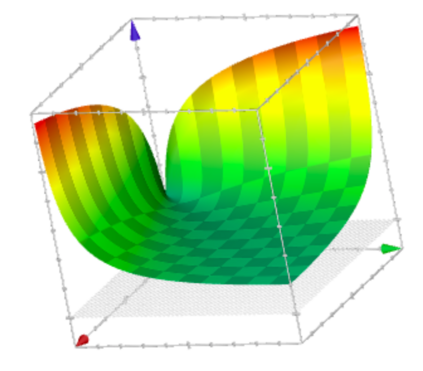
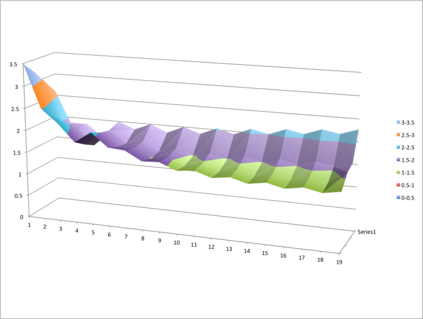
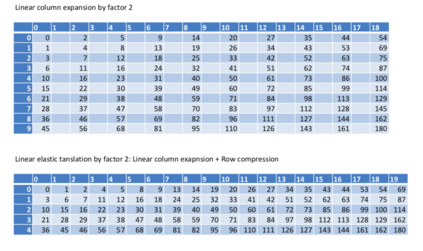
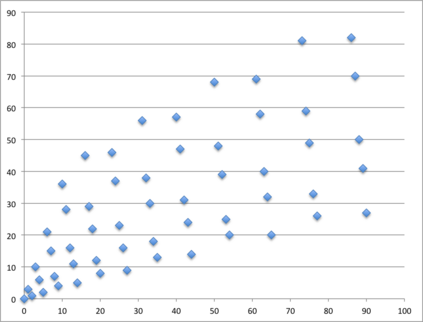
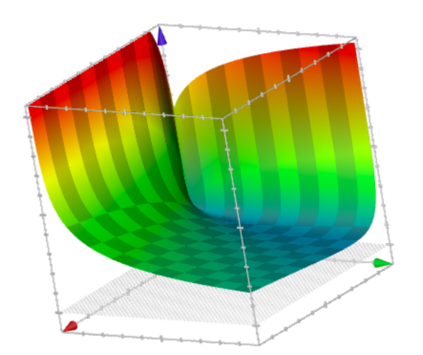
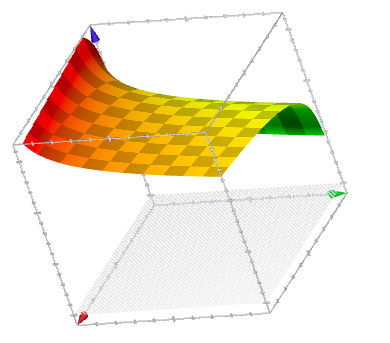
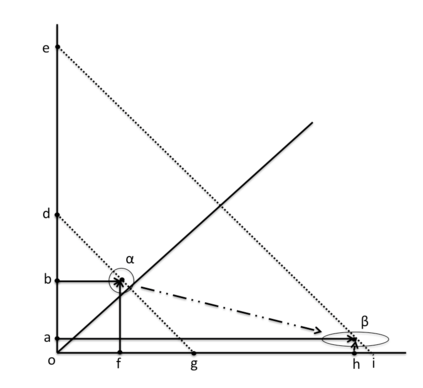
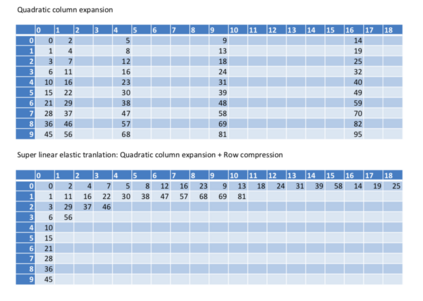
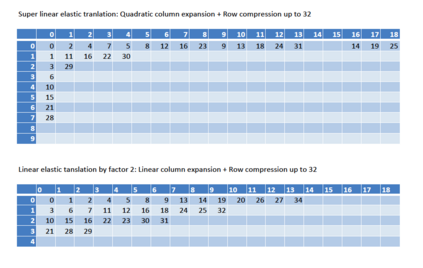
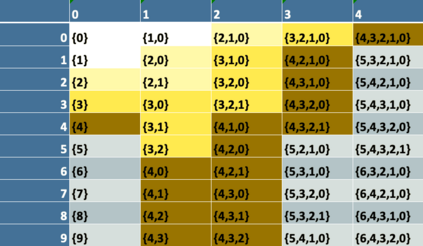
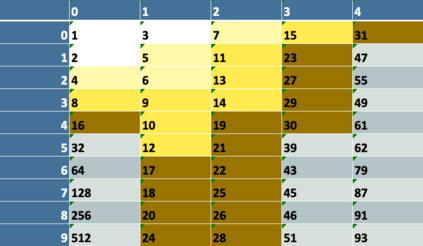
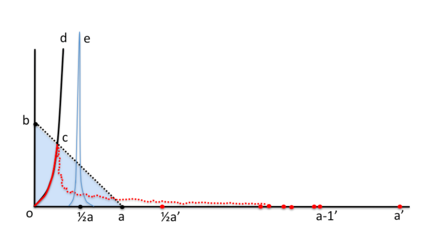
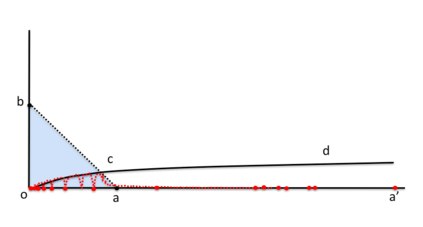
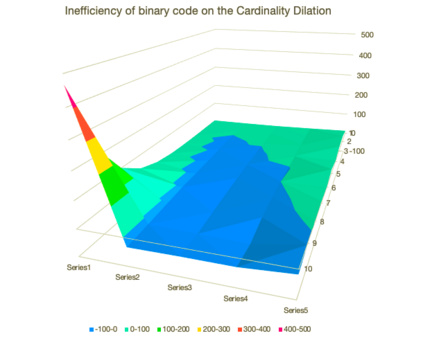
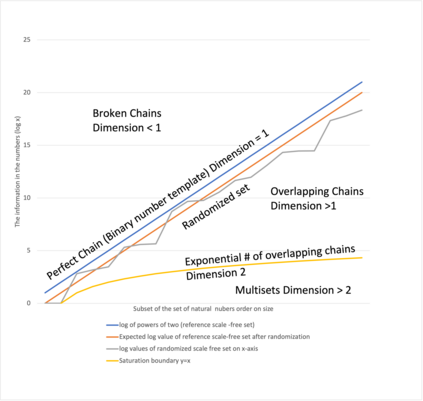
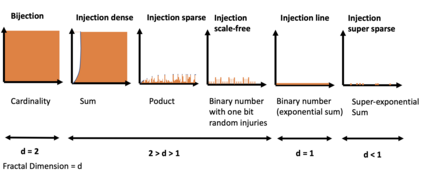
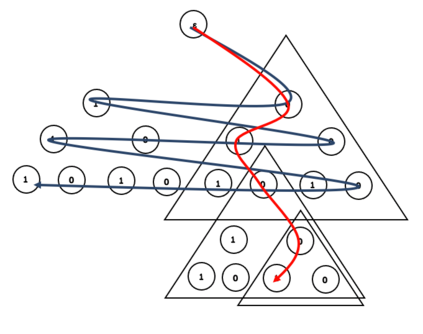
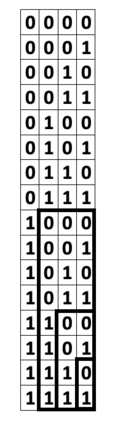
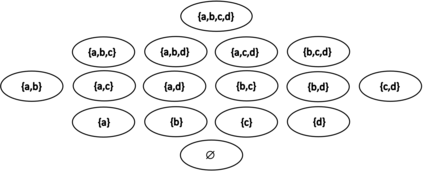
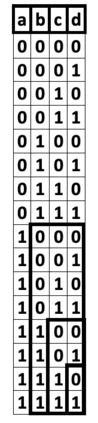
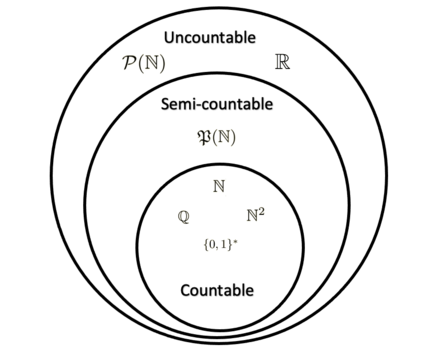
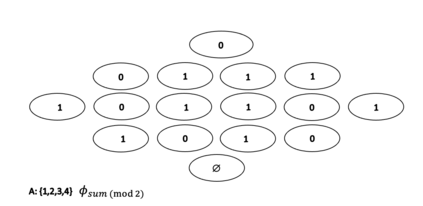
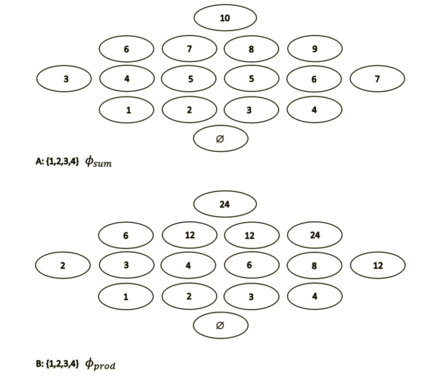
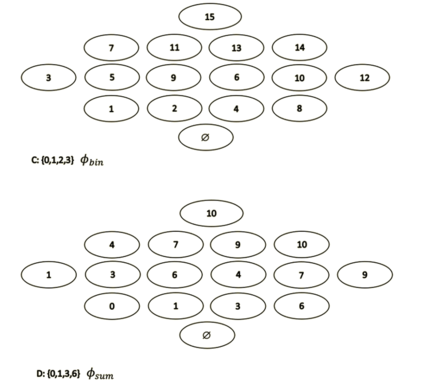
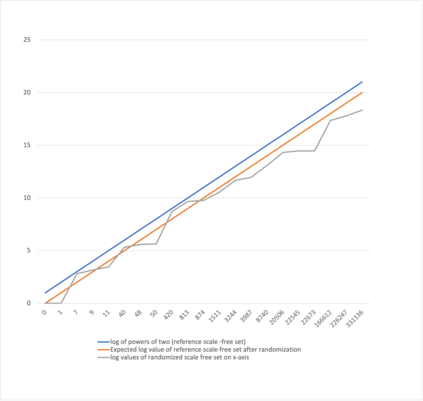
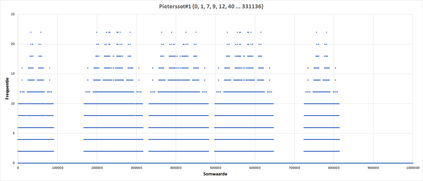
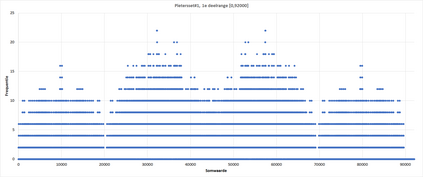
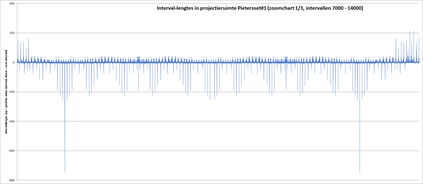
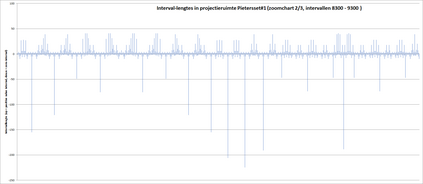
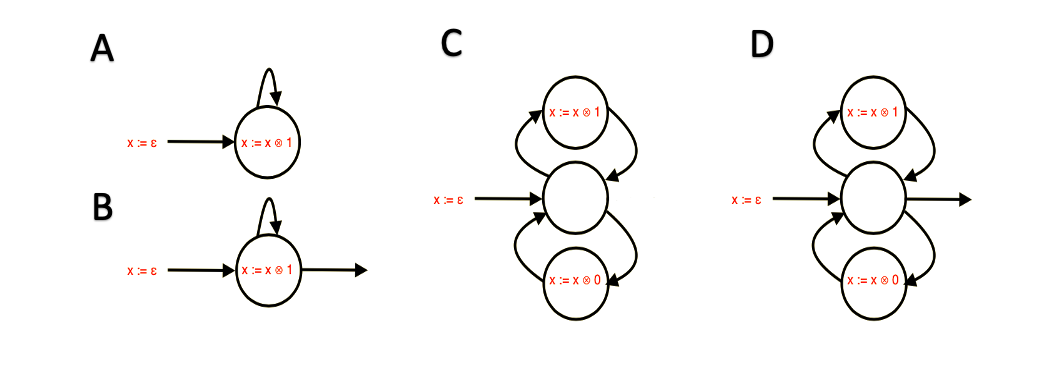
This paper presents a new foundational approach to information theory based on the concept of the information efficiency of a recursive function, which is defined as the difference between the information in the input and the output. The theory allows us to study planar representations of various infinite domains. Dilation theory studies the information effects of recursive operations in terms of topological deformations of the plane. I show that the well-known class of finite sets of natural numbers behaves erratically under such transformations. It is subject to phase transitions that in some cases have a fractal nature. The class is \emph{semi-countable}: there is no intrinsic information theory for this class and there are no efficient methods for systematic search. There is a relation between the information efficiency of the function and the time needed to compute it: a deterministic computational process can destroy information in linear time, but it can only generate information at logarithmic speed. Checking functions for problems in $NP$ are information discarding. Consequently, when we try to solve a decision problem based on an efficiently computable checking function, we need exponential time to reconstruct the information destroyed by such a function. At the end of the paper I sketch a systematic taxonomy for problems in $NP$.
翻译:暂无翻译