Self-Adjusting Linear Networks with Ladder Demand Graph

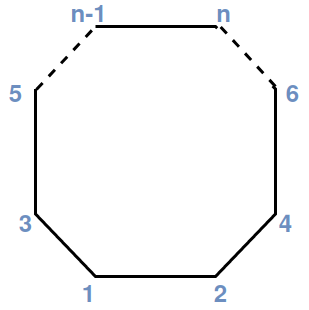
This paper revisits the problem of designing online algorithms for self-adjusting linear networks which dynamically adapt to the traffic pattern they serve. We refer to the graph formed by the pairwise communication requests as the demand graph. Even though the line is a fundamental network topology, existing results only study linear demand graphs. In this work, we take a first step toward studying more general demand graphs. We present a self-adjusting algorithm that responds to the traffic pattern drawn from the n-ladder graph%, i.e., a $2 \times n$ grid. The resulting algorithm appears to have an optimal competitive ratio. As two additional side results, we get a generic algorithm for an arbitrary demand graph and an optimal algorithm for a cycle demand graph.