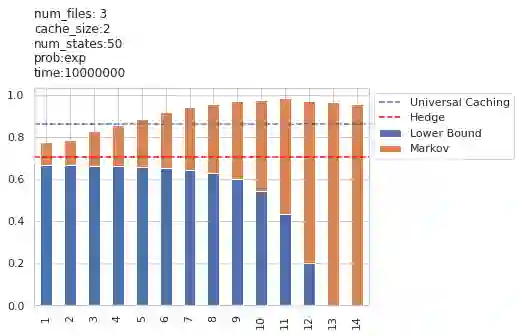
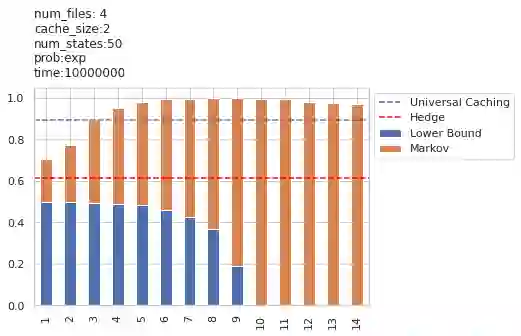
In the learning literature, the performance of an online policy is commonly measured in terms of the static regret metric, which compares the cumulative loss of an online policy to that of an optimal benchmark in hindsight. In the definition of static regret, the benchmark policy remains fixed throughout the time horizon. Naturally, the resulting regret bounds become loose in non-stationary settings where fixed benchmarks often suffer from poor performance. In this paper, we investigate a stronger notion of regret minimization in the context of an online caching problem. In particular, we allow the action of the offline benchmark at any round to be decided by a finite state predictor containing arbitrarily many states. Using ideas from the universal prediction literature in information theory, we propose an efficient online caching policy with an adaptive sub-linear regret bound. To the best of our knowledge, this is the first data-dependent regret bound known for the universal caching problem. We establish this result by combining a recently-proposed online caching policy with an incremental parsing algorithm, e.g., Lempel-Ziv '78. Our methods also yield a simpler learning-theoretic proof of the improved regret bound as opposed to the more involved and problem-specific combinatorial arguments used in the earlier works.
翻译:在学习文献中,在线政策的表现通常以静态遗憾衡量,将在线政策的累积损失与事后观察的最佳基准相比较。在静态遗憾的定义中,基准政策在整个时间跨度中保持不变。自然,由此产生的遗憾界限在非静止环境中变得松散,因为固定基准往往表现不佳。在本文中,我们调查了在网上缓冲问题背景下一个更强烈的遗憾最小化概念。特别是,我们允许任何回合的离线基准由含有任意性许多国家的限定状态预测器决定的行动。在信息理论中,我们使用普遍预测文献中的观点,我们提议一项有效的在线缓冲政策,并带有适应性的子线性遗憾束缚。据我们所知,这是已知的首个以数据为依存的遗憾在非静止环境中,而普遍缓冲问题又存在。我们通过将最近推出的在线缓冲政策与渐进式算法(例如,Lempel-Ziv'78)相结合,从而得出了这一结果。我们的方法还产生了一个较简单的学习理论证据,即改进的后悔力约束,而不是更早使用的问题。