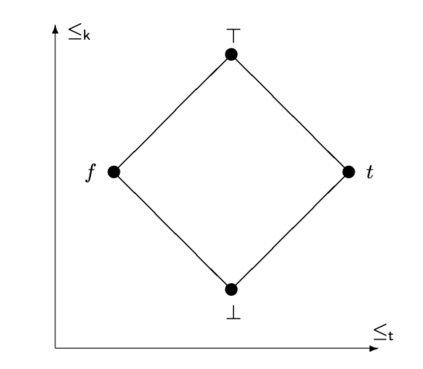
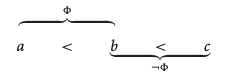
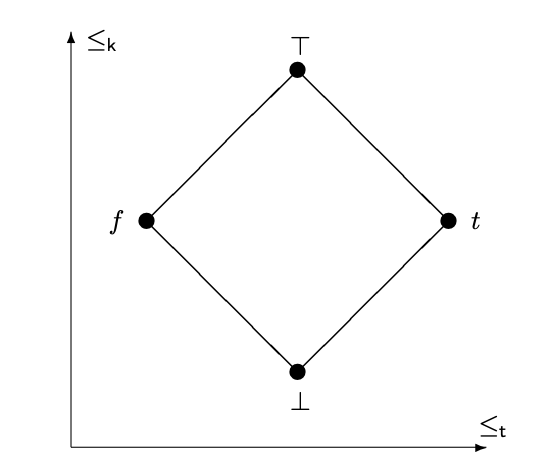
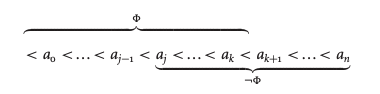It is argued that 4-valued paraconsistent truth values (called here "p-bits") can serve as a conceptual, mathematical and practical foundation for highly AI-relevant forms of probabilistic logic and probabilistic programming and concept formation. First it is shown that appropriate averaging-across-situations and renormalization of 4-valued p-bits operating in accordance with Constructible Duality (CD) logic yields PLN (Probabilistic Logic Networks) strength-and-confidence truth values. Then variations on the Curry-Howard correspondence are used to map these paraconsistent and probabilistic logics into probabilistic types suitable for use within dependent type based programming languages. Zach Weber's paraconsistent analysis of the sorites paradox is extended to form a paraconsistent / probabilistic / fuzzy analysis of concept boundaries; and a paraconsistent version of concept formation via Formal Concept Analysis is presented, building on a definition of fuzzy property-value degrees in terms of relative entropy on paraconsistent probability distributions. These general points are fleshed out via reference to the realization of probabilistic reasoning and programming and concept formation in the OpenCog AGI framework which is centered on collaborative multi-algorithm updating of a common knowledge metagraph.
翻译:据认为,四价半相容的真理价值(称为此处的“p-bits”)可以作为高度AI相关形式的概率逻辑和概率性编程和概念形成的概念、数学和实用基础;首先,可以证明,按照可建性Dqual(CD)逻辑运作的四价半相容的真理价值,可以产生PLN(概率逻辑网络)的强力和信心真相价值;然后,利用咖喱-榴弹通信的变异性,将这些相容性和概率性逻辑描绘成适合在依赖性编程语言范围内使用的高度AI相关形式的概率性逻辑。Zach Weber对索美主义悖论的相宜性分析扩展,形成对概念界限的准兼容性/概率/模糊性分析;通过正式概念分析提出概念形成概念的准兼容性版本,以相对性地产价值等级定义为基础,在准同性概率概率逻辑的相对参照值方面,将这种逻辑描绘成适合在依赖性编程语言中使用的概率性类型。Zach Weber对四价的相比分析扩展,将形成一个共同编程框架。