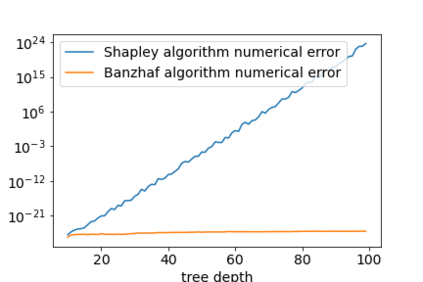
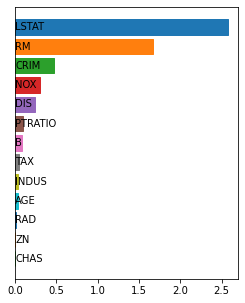
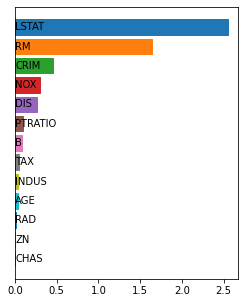
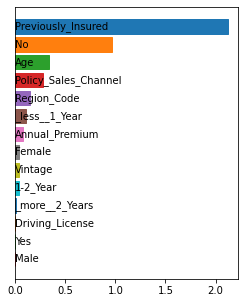
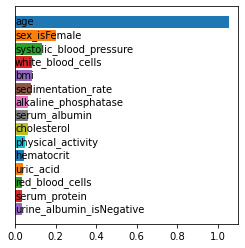
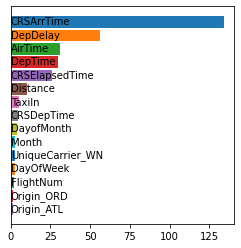
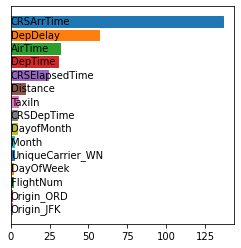
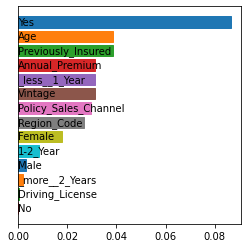
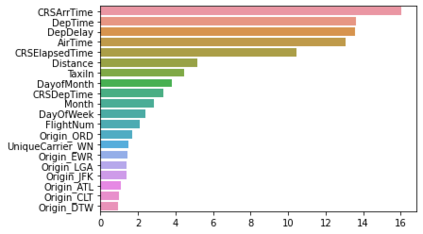
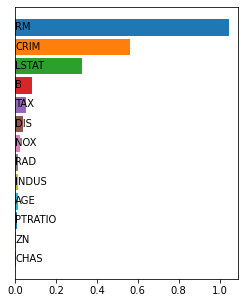
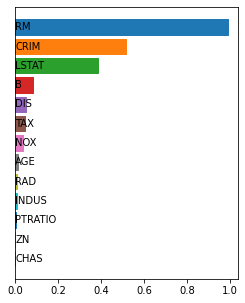
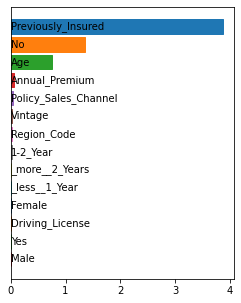
Shapley values are one of the main tools used to explain predictions of tree ensemble models. The main alternative to Shapley values are Banzhaf values that have not been understood equally well. In this paper we make a step towards filling this gap, providing both experimental and theoretical comparison of these model explanation methods. Surprisingly, we show that Banzhaf values offer several advantages over Shapley values while providing essentially the same explanations. We verify that Banzhaf values: (1) have a more intuitive interpretation, (2) allow for more efficient algorithms, and (3) are much more numerically robust. We provide an experimental evaluation of these theses. In particular, we show that on real world instances. Additionally, from a theoretical perspective we provide new and improved algorithm computing the same Shapley value based explanations as the algorithm of Lundberg et al. [Nat. Mach. Intell. 2020]. Our algorithm runs in $O(TLD+n)$ time, whereas the previous algorithm had $O(TLD^2+n)$ running time bound. Here, $T$ is the number of trees, $L$ is the maximum number of leaves in a tree, and $D$ denotes the maximum depth of a tree in the ensemble. Using the computational techniques developed for Shapley values we deliver an optimal $O(TL+n)$ time algorithm for computing Banzhaf values based explanations. In our experiments these algorithms give running times smaller even by an order of magnitude.
翻译:Shapley 值是用来解释对树共同值模型预测的主要工具之一。 Shapley 值的主要替代办法是 Banzhaf 值, 这些数值没有得到同等的理解。 在本文中, 我们为填补这一差距迈出了一步, 提供了对这些模型解释方法的实验性和理论性比较。 令人惊讶的是, 我们显示 Banzhaf 值比Shapley 值具有若干优势, 同时提供了基本相同的解释。 我们核实Banzhaf 值:(1) 具有更直观的解释, (2) 允许更高效的算法, (3) 数字性强得多。 我们对这些值进行了实验性评估。 我们特别在真实世界实例中展示了这一点。 此外, 我们从理论角度提供了新的和改进的算法, 计算与Lundberg 和 Al. [Nat. Mach. Intell. 2020] 的算法相同。 我们的算法以$( TLD+n) 值运行时间, 而以前的算法甚至用$( TLD2+n) 来设定时间约束。 这里, $ 美元是运行的树的运行量的计算值, 美元值, 美元, 使用一个最高值的计算方法的计算值值, 美元, 美元, 美元, 将使用一个最高值值的计算值值值值值值的计算。