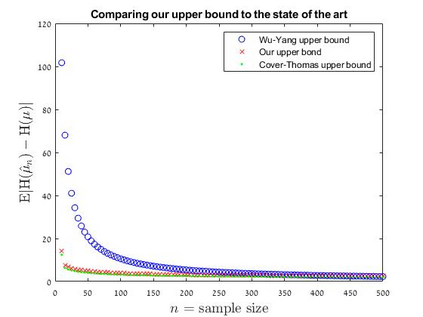
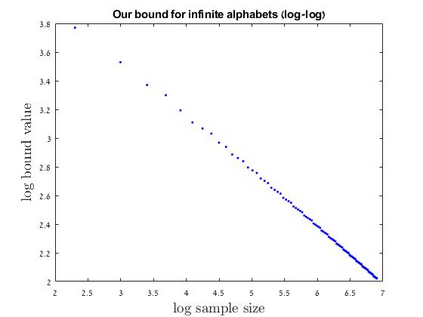
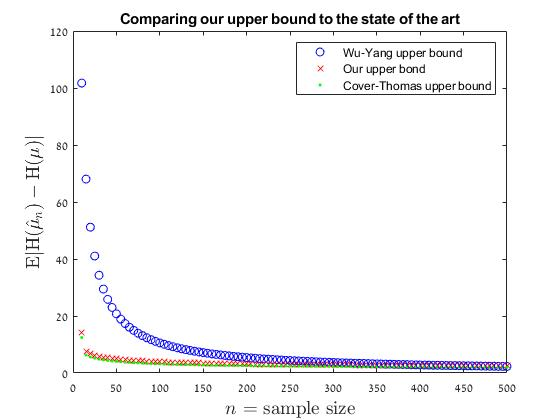
We seek an entropy estimator for discrete distributions with fully empirical accuracy bounds. As stated, this goal is infeasible without some prior assumptions on the distribution. We discover that a certain information moment assumption renders the problem feasible. We argue that the moment assumption is natural and, in some sense, {\em minimalistic} -- weaker than finite support or tail decay conditions. Under the moment assumption, we provide the first finite-sample entropy estimates for infinite alphabets, nearly recovering the known minimax rates. Moreover, we demonstrate that our empirical bounds are significantly sharper than the state-of-the-art bounds, for various natural distributions and non-trivial sample regimes. Along the way, we give a dimension-free analogue of the Cover-Thomas result on entropy continuity (with respect to total variation distance) for finite alphabets, which may be of independent interest. Additionally, we resolve all of the open problems posed by J\"urgensen and Matthews, 2010.
翻译:我们寻求一个具有充分实证准确度的离散分布估计值。 正如所述, 这一目标在没有事先对分布进行假设的情况下是行不通的。 我们发现, 某个信息时刻的假设使得问题变得可行。 我们认为, 时间假设是自然的, 在某些意义上, 极小的, 要比有限的支持或尾尾尾的衰变条件弱。 在目前假设下, 我们为无限字母提供了第一个有限smper 倍增估计值, 几乎恢复了已知的迷你马克思率。 此外, 我们证明, 我们的经验界限比最先进的界限, 各种自然分布和非三角抽样制度, 都明显亮得多。 沿着这条道路, 我们给限制字母( 与总变异距离有关) 的恒定连续性带来一个无维度的覆盖图象。 此外, 我们解决了2010年J\ “ urgensen” 和 Matthews 提出的所有公开问题。