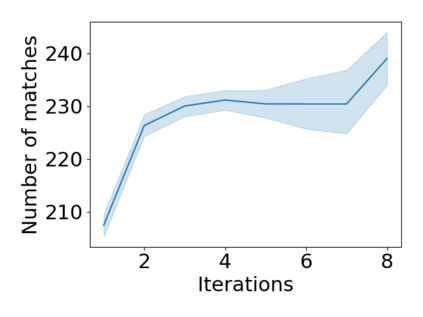
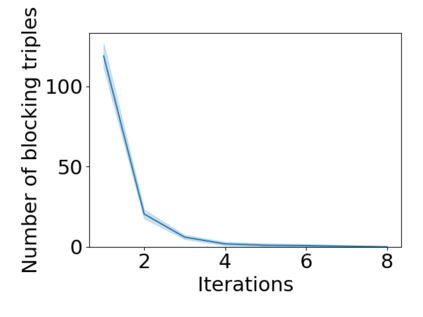
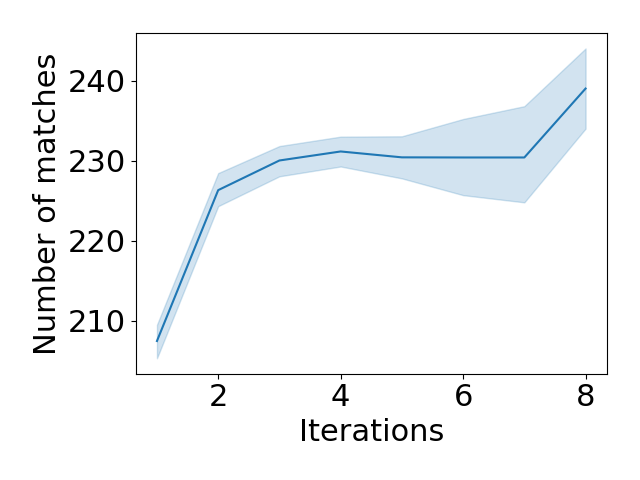
We introduce a new algorithm for finding stable matchings in multi-sided matching markets. Our setting is motivated by a PhD market of students, advisors, and co-advisors, and can be generalized to supply chain networks viewed as $n$-sided markets. In the three-sided PhD market, students primarily care about advisors and then about co-advisors (consistent preferences), while advisors and co-advisors have preferences over students only (hence they are cooperative). A student must be matched to one advisor and one co-advisor, or not at all. In contrast to previous work, advisor-student and student-co-advisor pairs may not be mutually acceptable (e.g., a student may not want to work with an advisor or co-advisor and vice versa). We show that three-sided stable matchings always exist, and present an algorithm that, in time quadratic in the market size (up to log factors), finds a three-sided stable matching using any two-sided stable matching algorithm as matching engine. We illustrate the challenges that arise when not all advisor-co-advisor pairs are compatible. We then generalize our algorithm to $n$-sided markets with quotas and show how they can model supply chain networks. Finally, we show how our algorithm outperforms the baseline given by [Danilov, 2003] in terms of both producing a stable matching and a larger number of matches on a synthetic dataset.
翻译:我们引入了一种在多面匹配市场寻找稳定匹配的新算法。 我们的设置是由学生、顾问和共同顾问的博士市场驱动的。 我们的设置可以推广到供应链网络中被视为美元面的市场。 在三面的博士市场中,学生主要关心顾问,然后关心共同顾问(一致的偏好 ), 而顾问和共同顾问只偏爱学生(因为他们是合作者 ) 。 学生必须匹配一位顾问和一位共同顾问,或者根本不匹配。 与以前的工作相比,顾问和学生-共同顾问的配对可能无法相互接受(例如,学生可能不想与顾问或共同顾问合作,反之亦然 ) 。 我们显示,三面的稳定匹配总是存在,而算法则在时间上对市场规模的四分立时,找到一个三面的稳定匹配,使用任何两面的稳定匹配算法作为匹配引擎。 我们举例说明了当不是所有顾问-共同学生和共同顾问的对等对等配对的对子可能无法相互接受的挑战(例如,学生可能不想与顾问或共同顾问或共同顾问或共同顾问合作顾问合作的对等,反的对等 ) 。 我们表明,一个稳定的2003年的连锁的配方的配方的配方的配方的配方的基价的网络是如何的基价的基价,我们展示了我们总的基的基价的基价的基价的基价是如何展示了我们的整个的基价的基价的基价是如何在2003年总的基价。