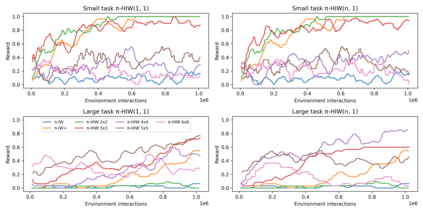
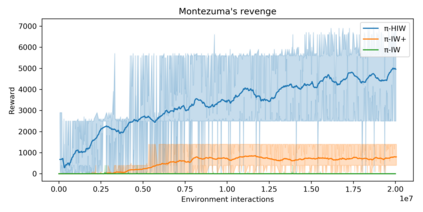
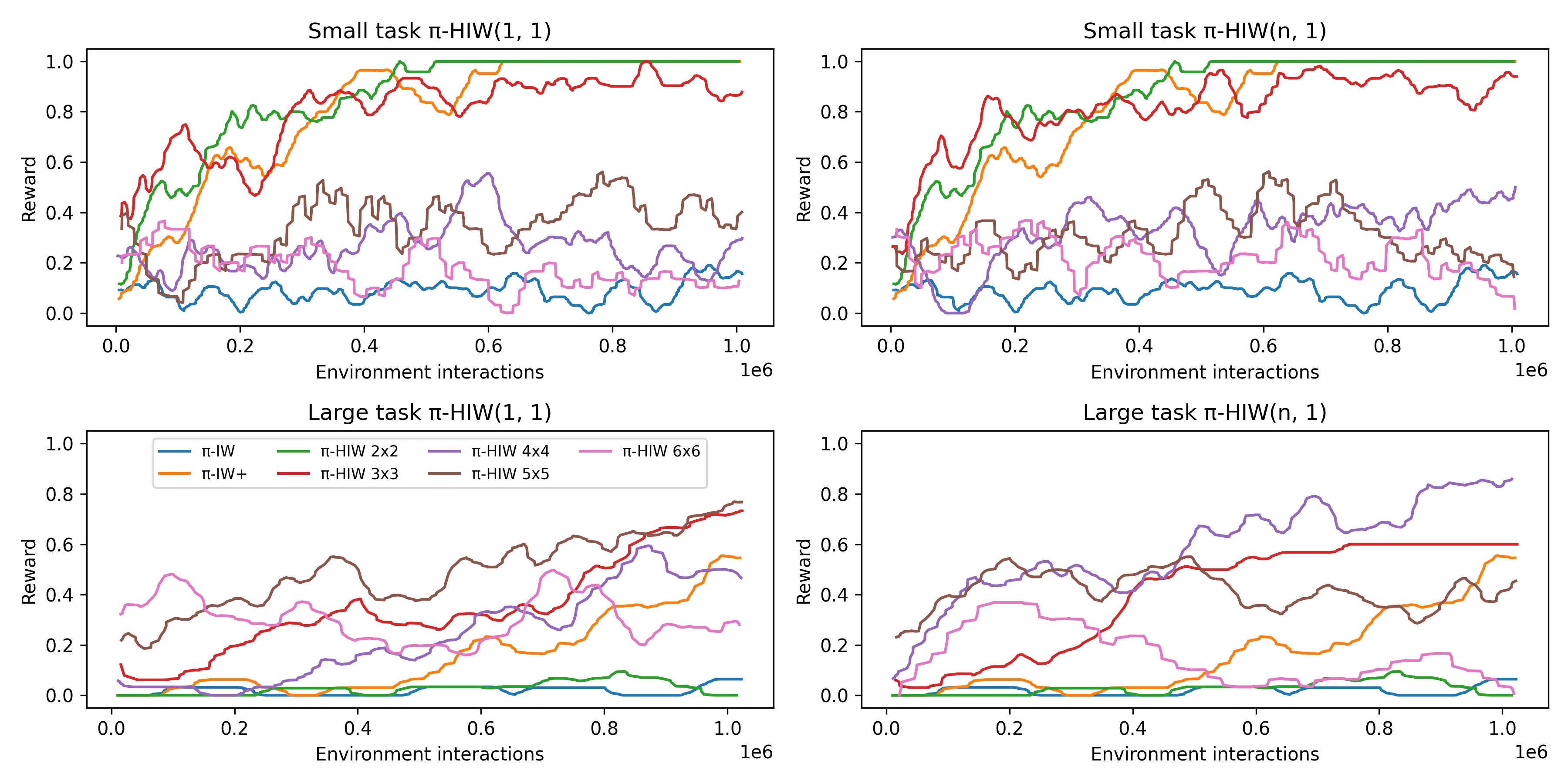
Width-based search methods have demonstrated state-of-the-art performance in a wide range of testbeds, from classical planning problems to image-based simulators such as Atari games. These methods scale independently of the size of the state-space, but exponentially in the problem width. In practice, running the algorithm with a width larger than 1 is computationally intractable, prohibiting IW from solving higher width problems. In this paper, we present a hierarchical algorithm that plans at two levels of abstraction. A high-level planner uses abstract features that are incrementally discovered from low-level pruning decisions. We illustrate this algorithm in classical planning PDDL domains as well as in pixel-based simulator domains. In classical planning, we show how IW(1) at two levels of abstraction can solve problems of width 2. For pixel-based domains, we show how in combination with a learned policy and a learned value function, the proposed hierarchical IW can outperform current flat IW-based planners in Atari games with sparse rewards.
翻译:基于宽度大于1的算法在计算上难以操作,禁止IW解决较高宽度的问题。在本文中,我们展示了一种分级算法,在两个层次上计划抽取。高层次规划员使用从低层次裁剪决定中逐渐发现的抽象特征。我们在经典规划 PDDL 域和以像素模拟器域中演示了这种算法。在经典规划中,我们展示了两种程度的抽象电算法如何解决宽度问题。2 在像素域中,我们展示了如何与一项学习的政策和一个学习的值函数相结合,拟议的等级IW可以比目前阿塔里游戏中以平板 IDDL 为基础的规划者少得分。