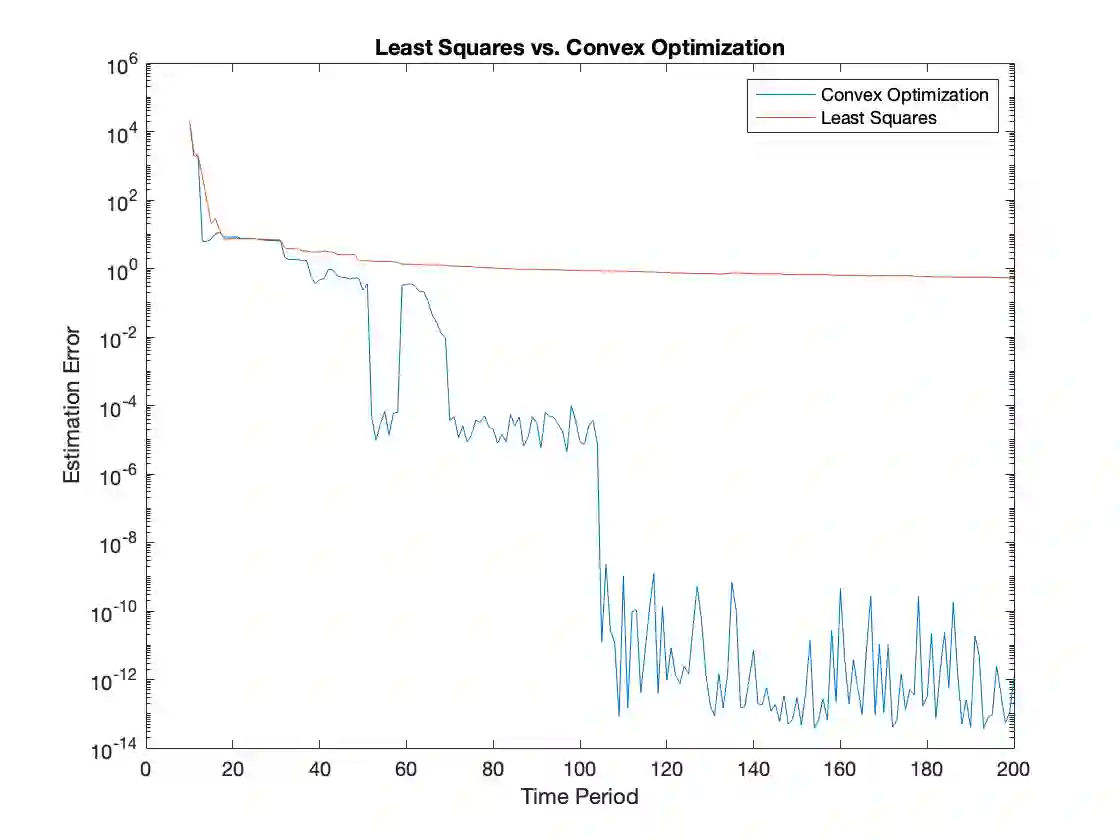
We study the identification of a linear time-invariant dynamical system affected by large-and-sparse disturbances modeling adversarial attacks or faults. Under the assumption that the states are measurable, we develop necessary and sufficient conditions for the recovery of the system matrices by solving a constrained lasso-type optimization problem. In addition, we provide an upper bound on the estimation error whenever the disturbance sequence is a combination of small noise values and large adversarial values. Our results depend on the null space property that has been widely used in the lasso literature, and we investigate under what conditions this property holds for linear time-invariant dynamical systems. Lastly, we further study the conditions for a specific probabilistic model and support the results with numerical experiments.
翻译:我们研究一个线性时变动态系统,它受到大规模和局部扰动模拟对抗性攻击或断层的影响。假设各州是可测量的,我们通过解决受限制的拉索型优化问题,为系统矩阵的恢复创造必要和充分的条件。此外,当扰动序列是小噪音值和大型对立值的结合时,我们提供估算误差的上限。我们的结果取决于在拉索文献中广泛使用的空空间财产,我们调查这些财产在什么条件下对线性时变动态系统持有何种条件。最后,我们进一步研究具体概率模型的条件,并以数字实验支持结果。