Stochastic Second-Order Methods Provably Beat SGD For Gradient-Dominated Functions

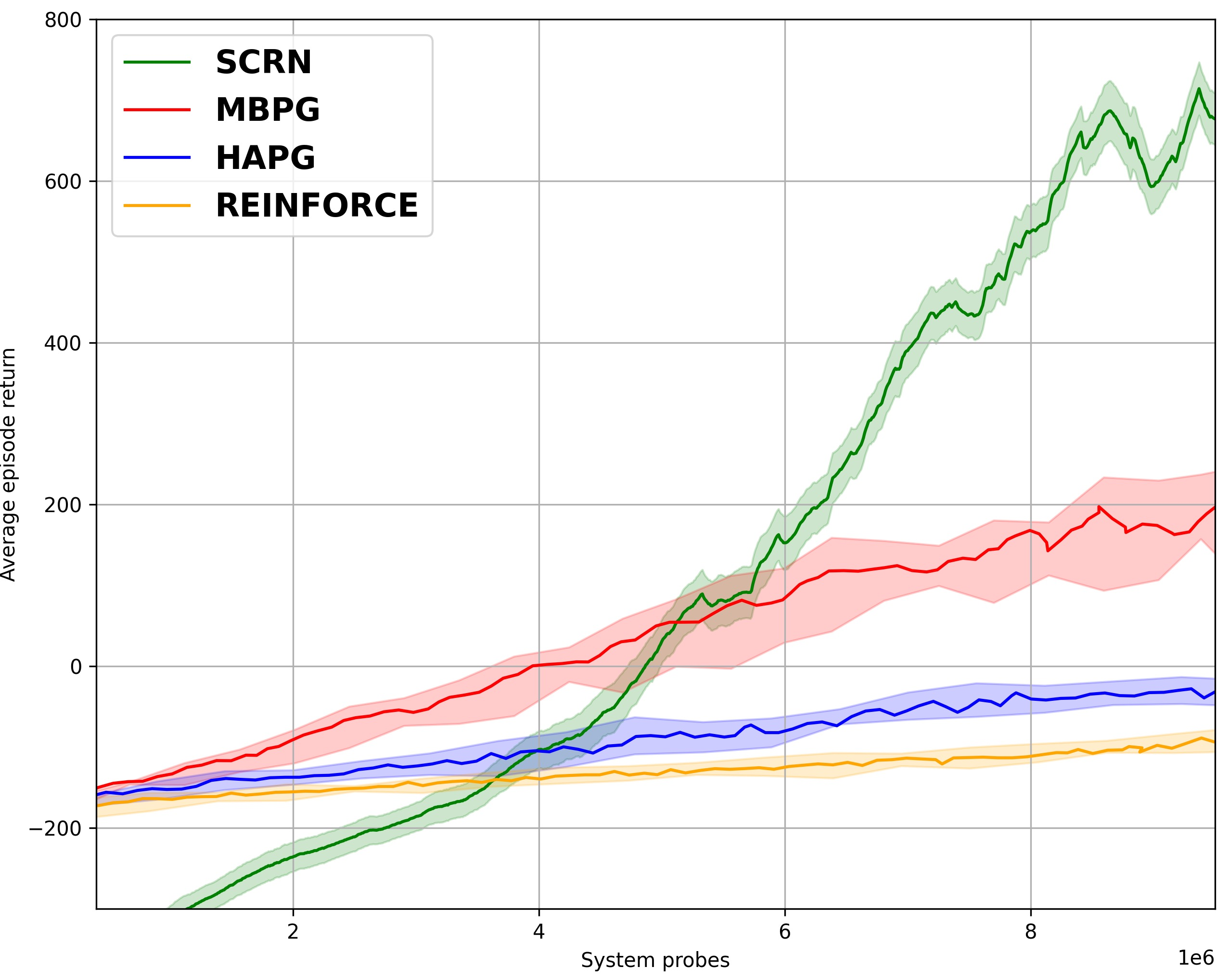
We study the performance of Stochastic Cubic Regularized Newton (SCRN) on a class of functions satisfying gradient dominance property which holds in a wide range of applications in machine learning and signal processing. This condition ensures that any first-order stationary point is a global optimum. We prove that SCRN improves the best-known sample complexity of stochastic gradient descent in achieving $\epsilon$-global optimum by a factor of $\mathcal{O}(\epsilon^{-1/2})$. Even under a weak version of gradient dominance property, which is applicable to policy-based reinforcement learning (RL), SCRN achieves the same improvement over stochastic policy gradient methods. Additionally, we show that the sample complexity of SCRN can be improved by a factor of ${\mathcal{O}}(\epsilon^{-1/2})$ using a variance reduction method with time-varying batch sizes. Experimental results in various RL settings showcase the remarkable performance of SCRN compared to first-order methods.