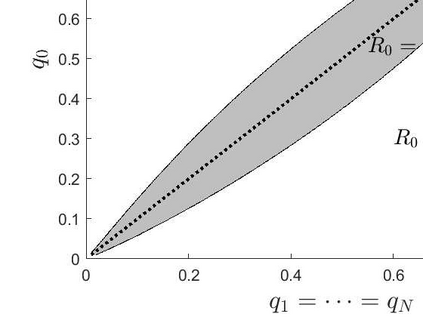
Consider a Bayesian binary decision-making problem in star networks, where local agents make selfish decisions independently, and a fusion agent makes a final decision based on aggregated decisions and its own private signal. In particular, we assume all agents have private beliefs for the true prior probability, based on which they perform Bayesian decision making. We focus on the Bayes risk of the fusion agent and counterintuitively find that incorrect beliefs could achieve a smaller risk than that when agents know the true prior. It is of independent interest for sociotechnical system design that the optimal beliefs of local agents resemble human probability reweighting models from cumulative prospect theory. We also consider asymptotic characterization of the optimal beliefs and fusion agent's risk in the number of local agents. We find that the optimal risk of the fusion agent converges to zero exponentially fast as the number of local agents grows. Furthermore, having an identical constant belief is asymptotically optimal in the sense of the risk exponent. For additive Gaussian noise, the optimal belief turns out to be a simple function of only error costs and the risk exponent can be explicitly characterized.
翻译:考虑恒星网络中的贝叶斯二进制决策问题, 当地代理人独立做出自私的决定, 融合剂根据综合决定和自己的私人信号做出最终决定。 特别是, 我们假设所有代理人都对真正的先前概率有私人信仰, 并以此为基础进行巴伊西亚决策。 我们关注聚变剂的贝耶斯风险, 并直觉地发现, 不正确的信念可能带来的风险比代理人知道真实之前的风险要小。 对于社会技术系统设计而言, 当地代理人的最佳信念类似于累积前景理论中的人类概率再加权模型。 我们还考虑对当地代理人中最佳信念和融合剂风险的简单定性。 我们发现, 聚变剂的最佳风险随着当地代理人数量的增加,会达到零倍速一致。 此外, 同样的一贯信念在风险推论的意义上是同样最理想的。 对于添加剂的噪音, 最理想的信念会变成一个简单的功能, 仅仅是错误成本和风险推算。