Clinical Utility Gains from Incorporating Comorbidity and Geographic Location Information into Risk Estimation Equations for Atherosclerotic Cardiovascular Disease

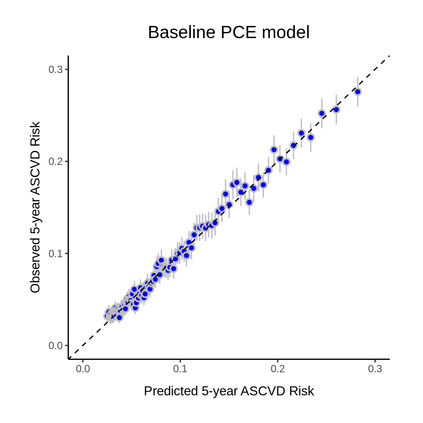
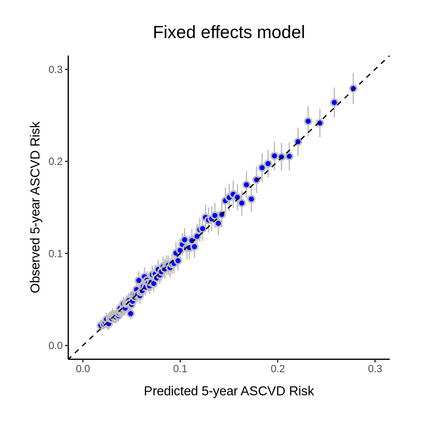
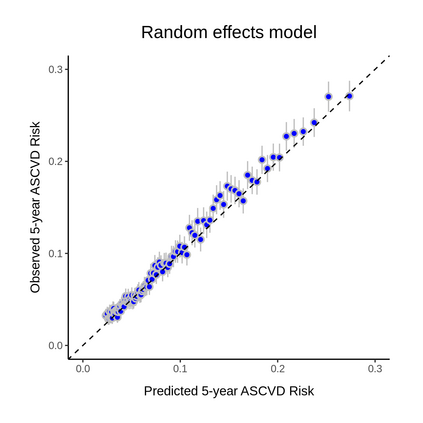
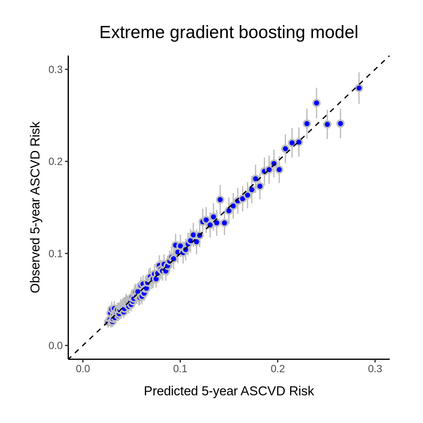
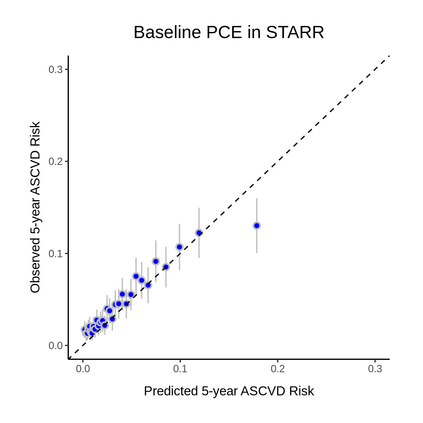
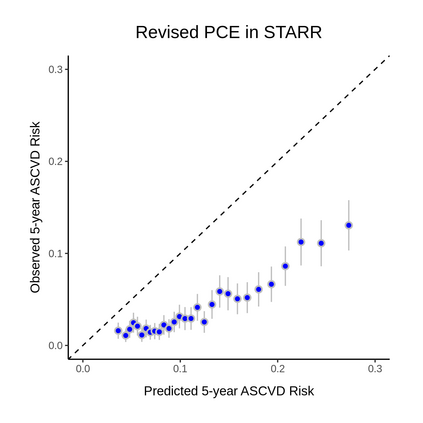
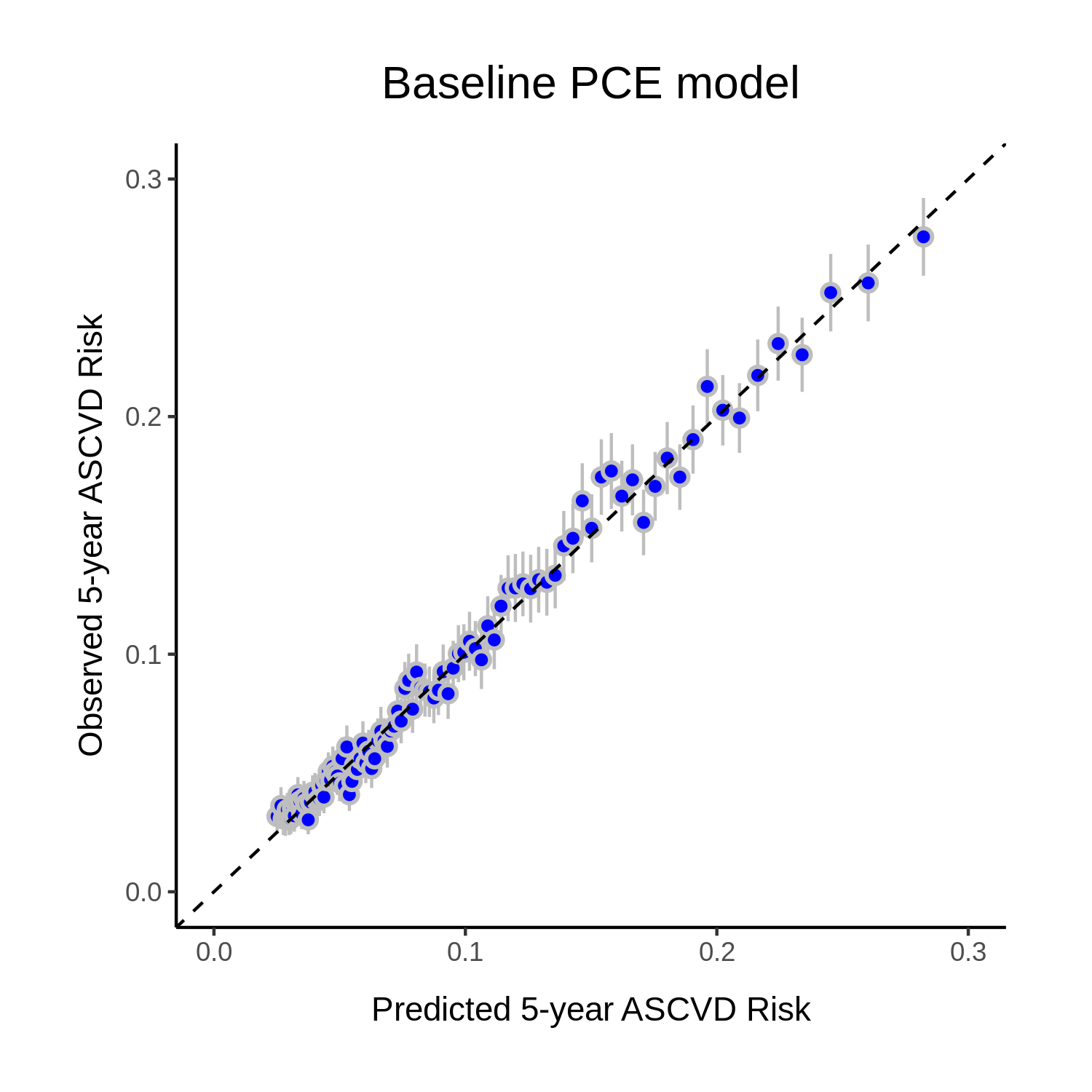
Objective: There are several efforts to re-learn the 2013 ACC/AHA pooled cohort equations (PCE) for patients with specific comorbidities and geographic locations. With over 363 customized risk models in the literature, we aim to evaluate such revised models to determine if the performance improvements translate to gains in clinical utility. Methods: We re-train a baseline PCE using the ACC/AHA PCE variables and revise it to incorporate subject-level geographic location and comorbidity information. We apply fixed effects, random effects, and extreme gradient boosting models to handle the correlation and heterogeneity induced by locations. Models are trained using 2,464,522 claims records from Optum Clinformatics Data Mart and validated in the hold-out set (N=1,056,224). We evaluate models' performance overall and across subgroups defined by the presence or absence of chronic kidney disease (CKD) or rheumatoid arthritis (RA) and geographic locations. We evaluate models' expected net benefit using decision curve analysis and models' statistical properties using several discrimination and calibration metrics. Results: The baseline PCE is miscalibrated overall, in patients with CKD or RA, and locations with small populations. Our revised models improved both the overall (GND P-value=0.41) and subgroup calibration but only enhanced net benefit in the underrepresented subgroups. The gains are larger in the subgroups with comorbidities and heterogeneous across geographic locations. Conclusions: Revising the PCE with comorbidity and location information significantly enhanced models' calibration; however, such improvements do not necessarily translate to clinical gains. Thus, we recommend future works to quantify the consequences from using risk calculators to guide clinical decisions.