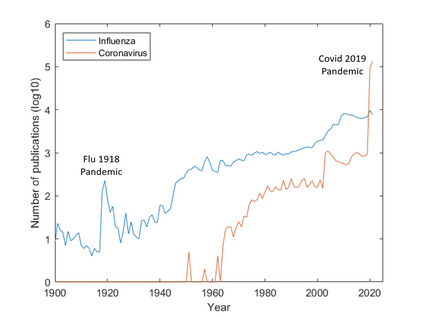
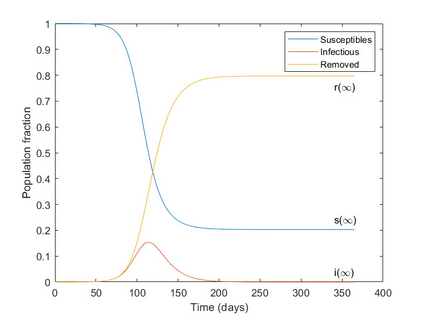
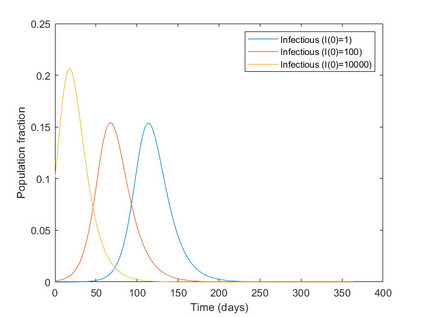
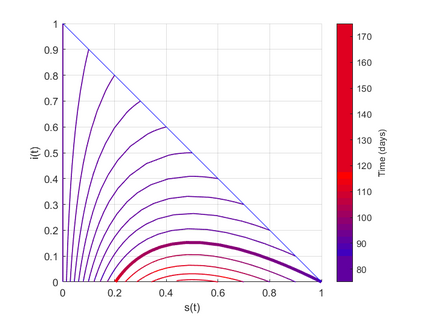
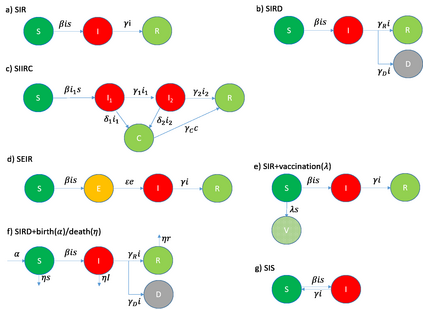
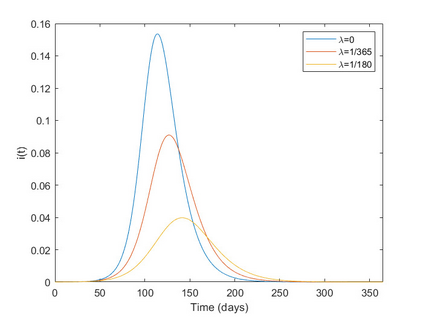
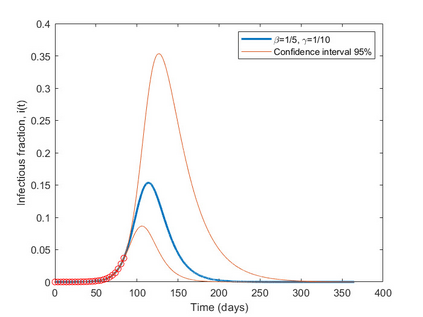
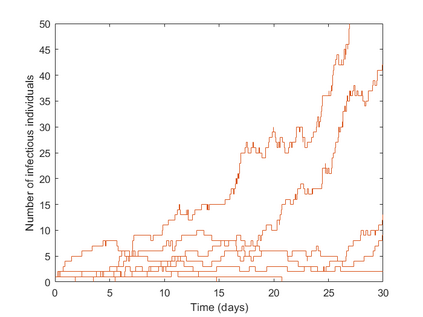
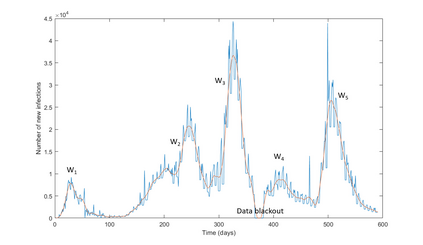
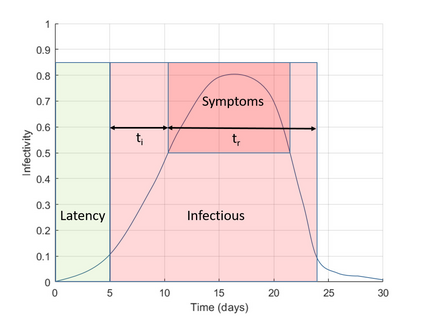
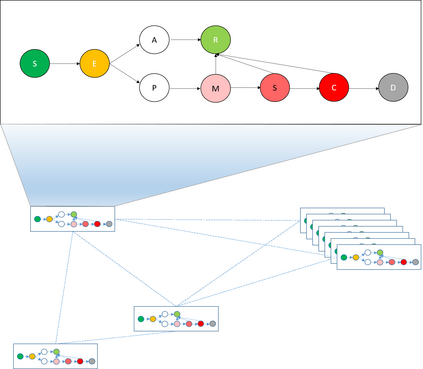
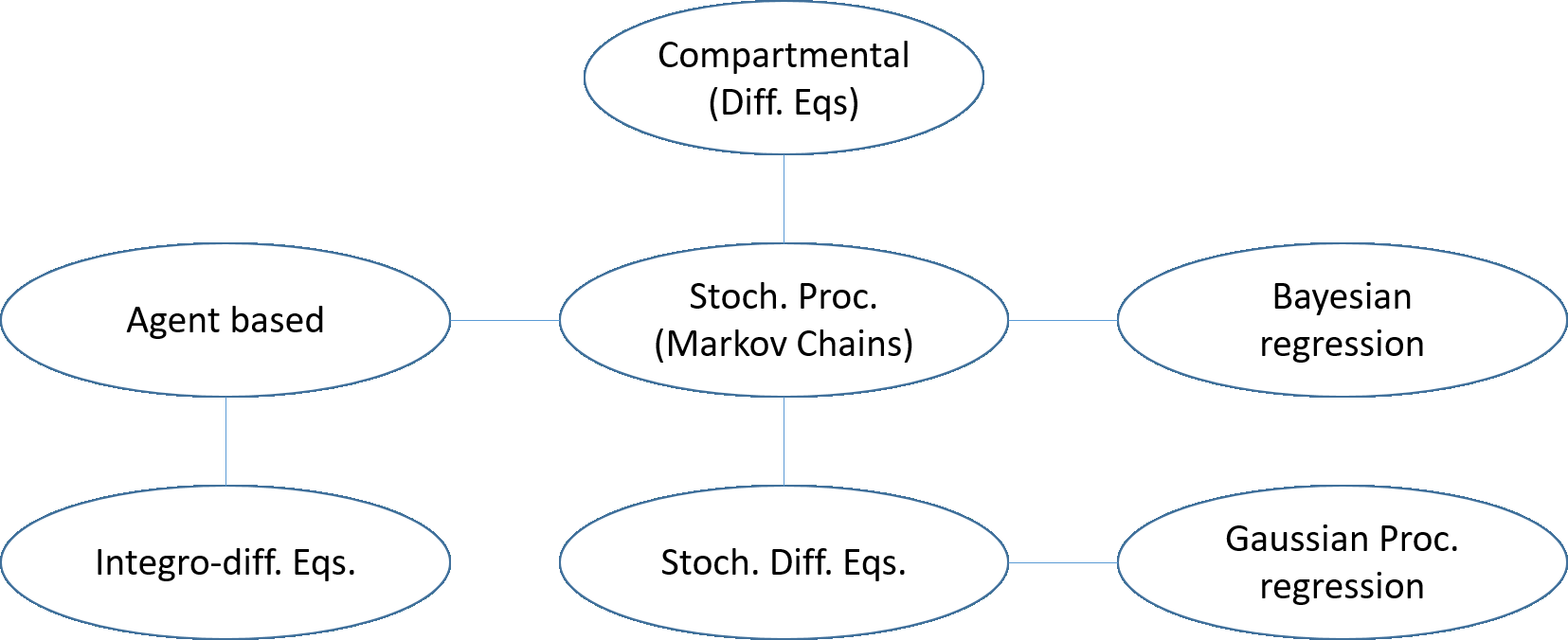
This article explores mathematical models for understanding the evolution of contagious diseases. The most widely known set of models are the compartmental ones, which are based on a set of differential equations. But these are not the only models. This review visits many different families of models. Additionally, we show these families, not as unrelated entities, but following a common thread in which the problems or assumptions of a model are solved or generalized by another model. In this way, we can understand their relationships, assumptions, simplifications, and, ultimately, limitations. Prompted by the current Covid19 pandemic, we have a special focus on spread forecasting. We illustrate the difficulties encountered to do realistic predictions. In general, they are only approximations to a reality whose biological and societal complexity is much larger. Particularly troublesome are the large underlying variability, the problem's time-varying nature, and the difficulty to estimate the required parameters for a faithful model. Additionally, we will also see that these models have a multiplicative nature implying that small errors in the system parameters cause a huge uncertainty in the prediction. Stochastic or agent-based models can overcome some of the modeling problems of systems based on differential or stochastic equations. Their main difficulty is that they are as accurate and realistic as the data available to estimate their detailed parametrization, and very often this detailed data is not at the modeller's disposal. Although the predictive power of mathematical models to forecast the evolution of a contagious disease is very limited, these models are still very useful to plan interventions as they can calculate their impact if all other parameters stay fixed. They are also very useful to understand the properties of disease propagation in complex systems.
翻译:文章探索了用于理解传染病演变的数学模型。 最广为人知的一组模型是基于一组差异方程式的条块式参数。 但是这些模型并不是唯一的模型。 本次审查访问的是许多不同的模型家庭。 此外, 我们展示这些家庭, 不是无关的实体, 而是遵循一个共同的线索, 其中模型的问题或假设通过另一个模型解决或普遍化。 这样, 我们就能理解它们的关系、 假设、 简化, 以及最终的局限性。 在当前Covid19年大流行的情况下, 我们特别注重传播预测。 我们展示了在进行现实预测时遇到的困难。 一般来说, 它们只是接近一个生物和社会复杂程度大得多的现实。 特别麻烦的是巨大的潜在变异性、 问题的时间变异性, 以及难以估计一个忠实模型所需要的参数。 此外, 我们还会看到这些模型具有多重的实用性, 意味着系统参数中的小错误仍然在预测中产生巨大的不确定性。 托科或代理人模型可以克服一些不切实际的模型, 这些模型在精确的变异性模型上, 它们的变异性模型是它们的精确性模型, 它们作为主要变异性模型的变异性模型, 也是其精确的精确的变异性模型, 它们的精确的, 它们的精确的变异性模型是其精确的, 的, 它们的精确的精确的, 它们是它们的精确的, 其精确的变异性变变变变的变的, 。