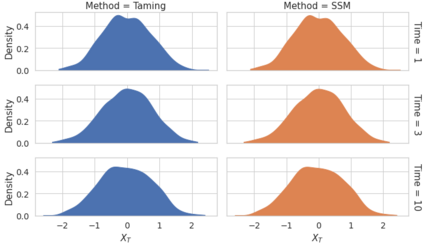
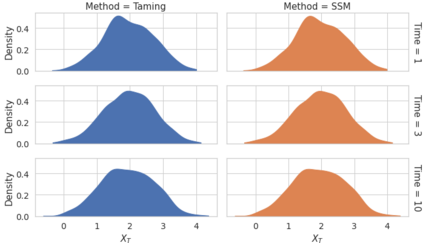
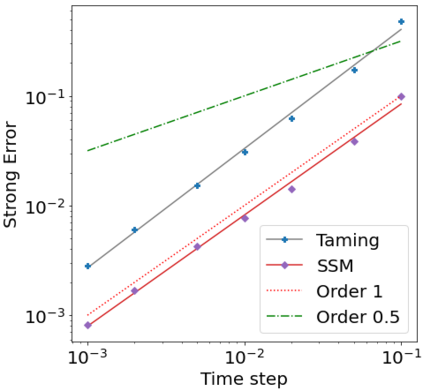
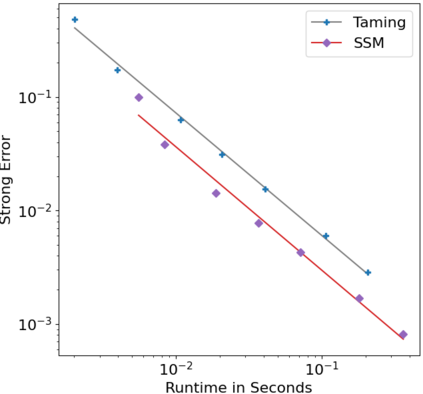
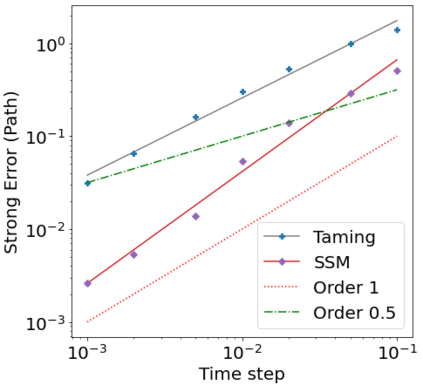
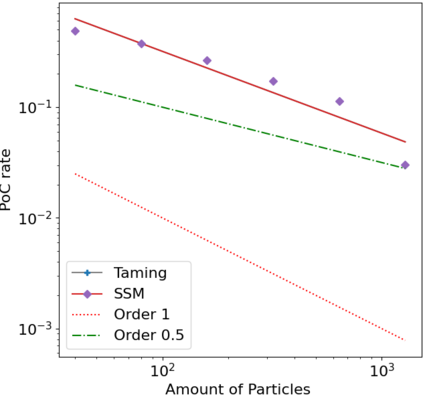
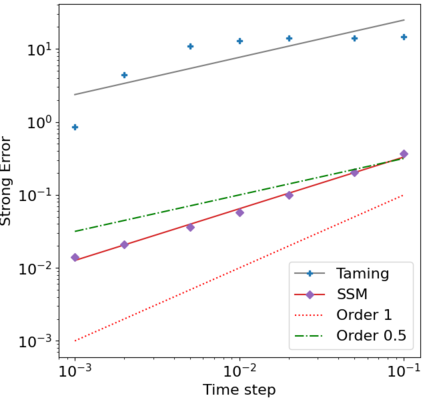
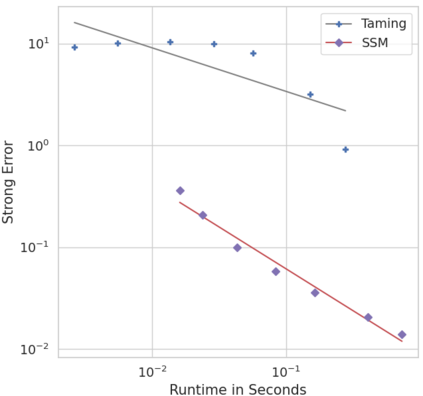
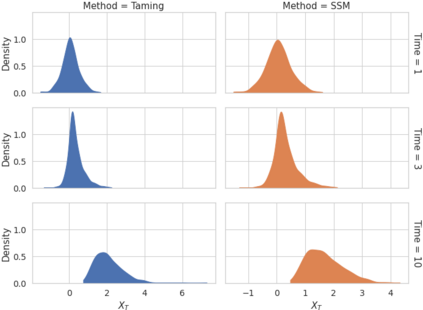
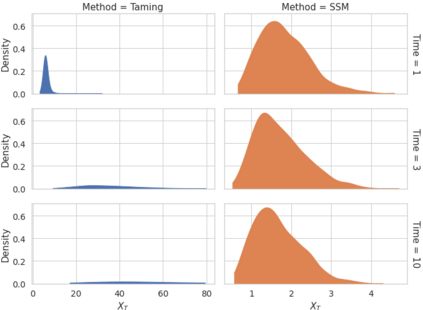
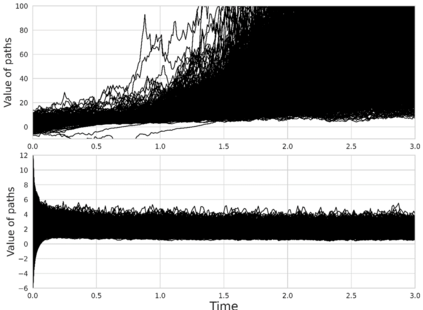
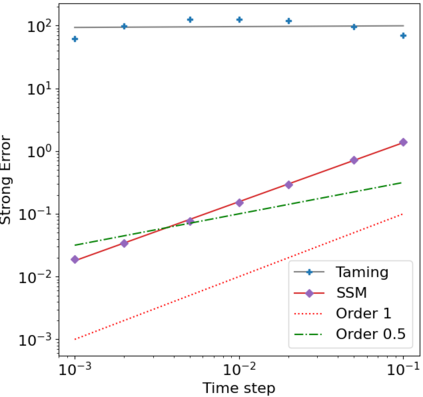
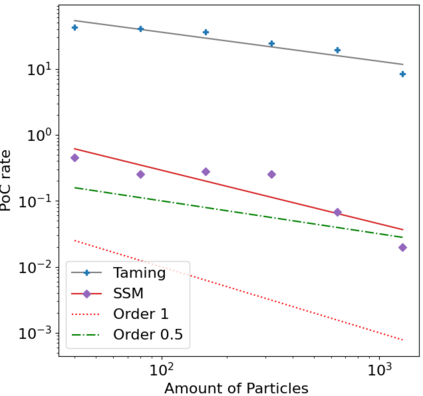
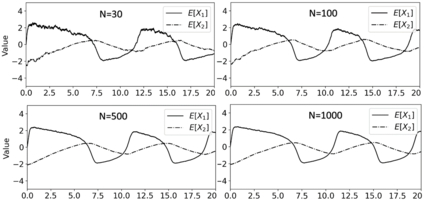
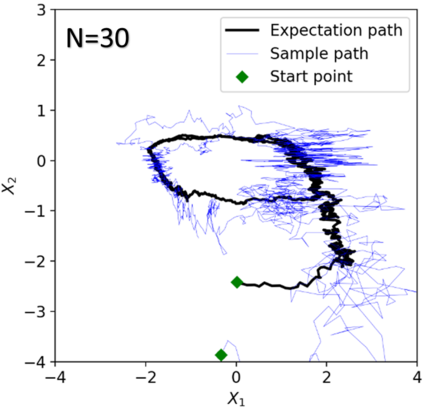
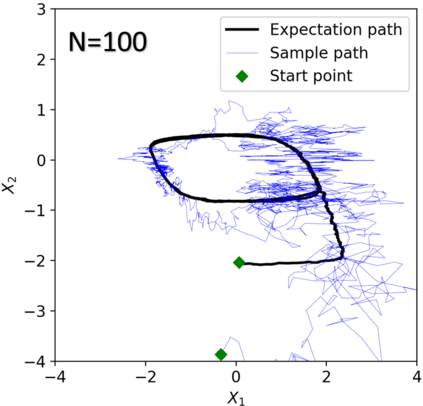
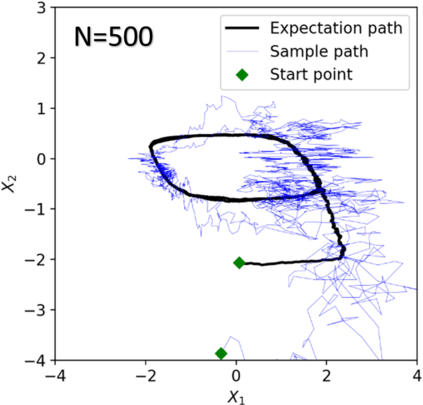
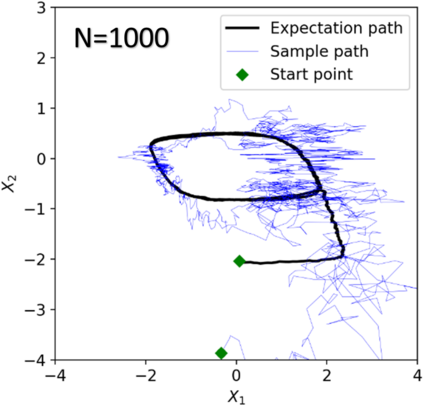
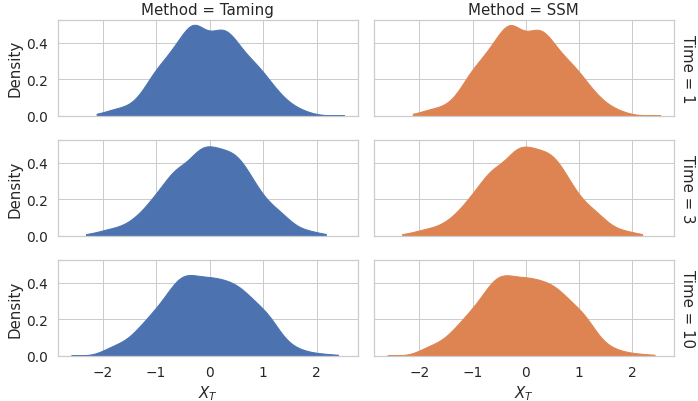
We consider in this work the convergence of a split-step Euler type scheme (SSM) for the numerical simulation of interacting particle Stochastic Differential Equation (SDE) systems and McKean-Vlasov Stochastic Differential Equations (MV-SDEs) with full super-linear growth in the spatial and the interaction component in the drift, and non-constant Lipschitz diffusion coefficient. The super-linear growth in the interaction (or measure) component stems from convolution operations with super-linear growth functions allowing in particular application to the granular media equation with multi-well confining potentials. From a methodological point of view, we avoid altogether functional inequality arguments (as we allow for non-constant non-bounded diffusion maps). The scheme attains, in stepsize, a near-optimal classical (path-space) root mean-square error rate of $1/2-\varepsilon$ for $\varepsilon>0$ and an optimal rate $1/2$ in the non-path-space mean-square error metric. Numerical examples illustrate all findings. In particular, the testing raises doubts if taming is a suitable methodology for this type of problem (with convolution terms and non-constant diffusion coefficients).
翻译:我们认为,在这项工作中,对交互式粒子粒子蒸汽分化(SDE)系统和McKan-Vlasov Stochatic Equations(MV-SDEs)系统进行数字模拟的分步Euler型计划(SSSM)和McKan-Vlasov Stochatic Equalations(MV-SDEs)系统(MV-SDEs),与漂移的空间和互动部分完全超线性增长和不固定的Lipschitz 扩散系数。互动(或计量)部分的超级线性增长来自具有超线性增长功能的连动操作,特别允许对具有多孔缩小潜力的颗粒媒体方程式应用。从方法的角度看,我们完全避免了功能上的不平等论点(因为我们允许不连续、无限制的分布式扩散分布式的分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式分布式图),在逐步化中,在1/2\varesil-valepalislluslllllusluslusluslluslusluslllluslusluslusluslonlonluslusluslonlusmlusmlusmlusmlusmluslusmlusmlusmlusmlusl) exlusmlusmlusmmmlex。