Information Geometry Approach to Parameter Estimation in Hidden Markov Models

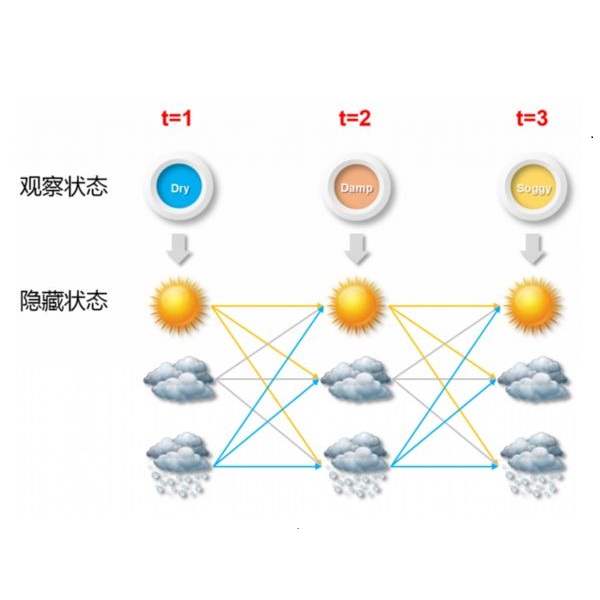
We consider the estimation of the transition matrix of a hidden Markovian process by using information geometry with respect to transition matrices. In this paper, only the histogram of $k$-memory data is used for the estimation. To establish our method, we focus on a partial observation model with the Markovian process and we propose an efficient estimator whose asymptotic estimation error is given as the inverse of projective Fisher information of transition matrices. This estimator is applied to the estimation of the transition matrix of the hidden Markovian process. In this application, we carefully discuss the equivalence problem for hidden Markovian process on the tangent space.