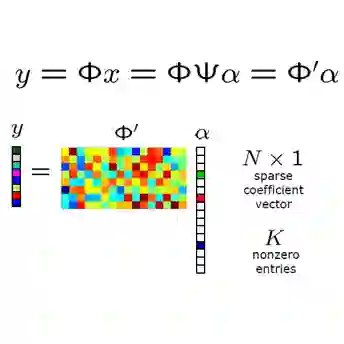
Growing set of optimization and regression techniques, based upon sparse representations of signals, to build models from data sets has received widespread attention recently with the advent of compressed sensing. This paper deals with the parameterization of the Lorenz-96 model with two time-scales that mimics mid-latitude atmospheric dynamics with microscopic convective processes. Compressed sensing is used to build models (vector fields) to emulate the behavior of the fine-scale process, so that explicit simulations become an online benchmark for parameterization. We apply compressed sensing, where the sparse recovery is achieved by constructing a sensing/dictionary matrix from ergodic samples generated by the Lorenz-96 atmospheric model, to parameterize the unresolved variables in terms of resolved variables. Stochastic parameterization is achieved by auto-regressive modelling of noise. We utilize the ensemble Kalman filter for data assimilation, where observations (direct measurements) are assimilated in the low-dimensional stochastic parameterized model to provide predictions. Finally, we compare the predictions of compressed sensing and Wilk's polynomial regression to demonstrate the potential effectiveness of the proposed methodology.
翻译:根据信号的微弱表现,为建立数据集模型而不断增长的优化和回归技术集基于信号的信号,最近随着压缩遥感的到来而引起广泛关注。本文件涉及Lorenz-96模型的参数化,该模型有两种时间尺度,以模拟中纬度大气动态和微粒相近过程。压缩的遥感用于建立模型(摄像场),以效仿微缩过程的行为,从而使明确的模拟成为参数化的在线基准。我们应用压缩遥感,通过从Lorenz-96大气模型产生的遗传样本中建立一种感测/字质矩阵,实现稀有的恢复,以便用溶解变量对尚未解决的变量进行参数化。存储参数化是通过噪音的自动反向建模实现的。我们利用高官Kalman过滤器进行数据同化,将观测(直接测量)同化到低度的随机测量参数化模型中以提供预测。最后,我们比较了压缩遥感预测和Wilk的多子回归,以证明拟议方法的潜在效力。