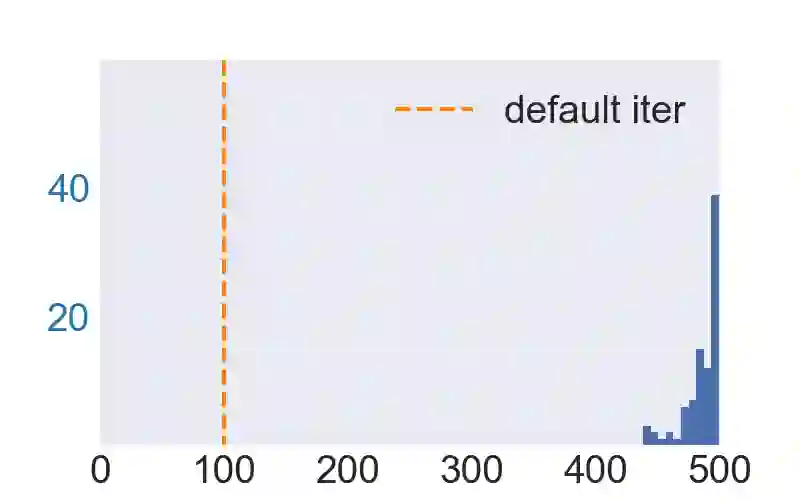
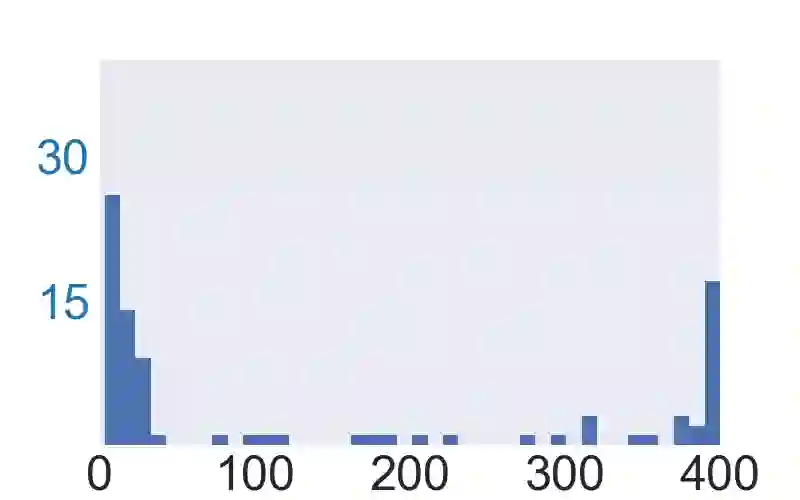
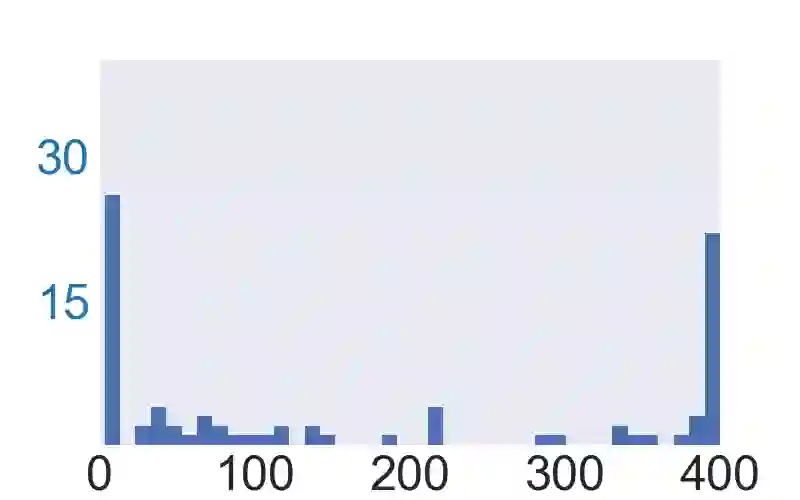
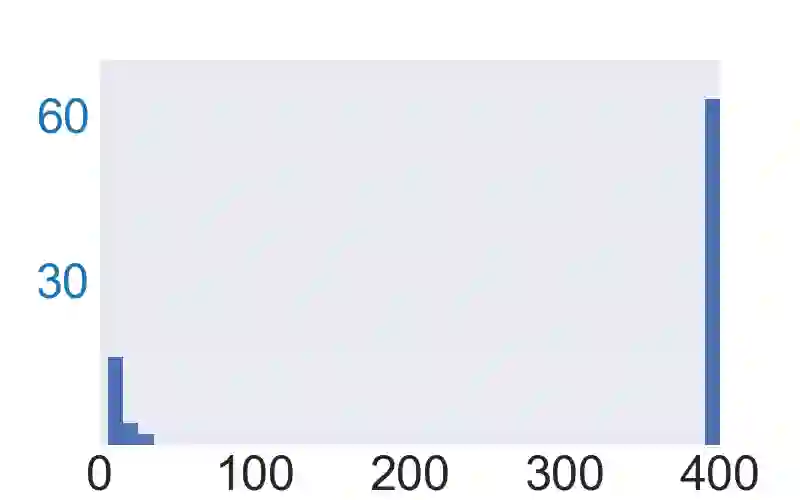
Empirical robustness evaluation (RE) of deep learning models against adversarial perturbations entails solving nontrivial constrained optimization problems. Existing numerical algorithms that are commonly used to solve them in practice predominantly rely on projected gradient, and mostly handle perturbations modeled by the $\ell_1$, $\ell_2$ and $\ell_\infty$ distances. In this paper, we introduce a novel algorithmic framework that blends a general-purpose constrained-optimization solver PyGRANSO with Constraint Folding (PWCF), which can add more reliability and generality to the state-of-the-art RE packages, e.g., AutoAttack. Regarding reliability, PWCF provides solutions with stationarity measures and feasibility tests to assess the solution quality. For generality, PWCF can handle perturbation models that are typically inaccessible to the existing projected gradient methods; the main requirement is the distance metric to be almost everywhere differentiable. Taking advantage of PWCF and other existing numerical algorithms, we further explore the distinct patterns in the solutions found for solving these optimization problems using various combinations of losses, perturbation models, and optimization algorithms. We then discuss the implications of these patterns on the current robustness evaluation and adversarial training.
翻译:深度学习模型在对抗扰动下的经验鲁棒性评估(RE)需要解决非常复杂的约束优化问题。目前在实践中常用的数值算法主要依赖于投影梯度,并且主要处理由 $\ell_1$,$\ell_2$ 和 $\ell_\infty$ 距离建模的扰动。在本文中,我们介绍了一种新的算法框架,将通用的约束优化求解器 PyGRANSO 与约束折叠(PWCF)相结合,可以为现有的RE包(如AutoAttack)增加更多可靠性和通用性。关于可靠性,PWCF提供具有稳定性度量和可行性测试的解来评估解质量。对于通用性,PWCF可以处理通常无法访问的扰动模型,其中的主要要求是距离度量几乎处处可微分。利用PWCF和其他现有的数值算法,我们进一步探讨了使用不同的损失、扰动模型和优化算法解决这些优化问题所发现的不同模式。然后我们讨论这些模式对当前的鲁棒性评估和对抗训练的影响。