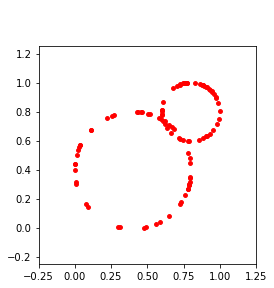
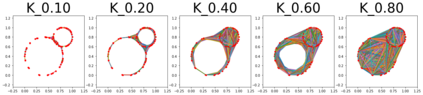
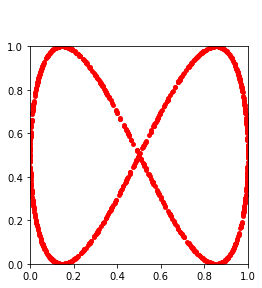
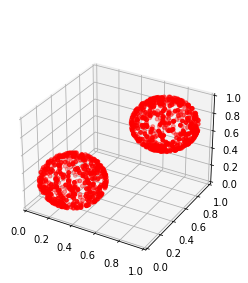
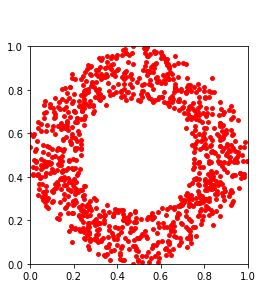
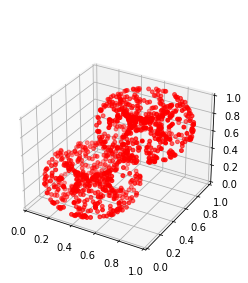
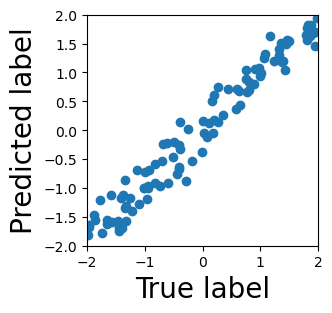
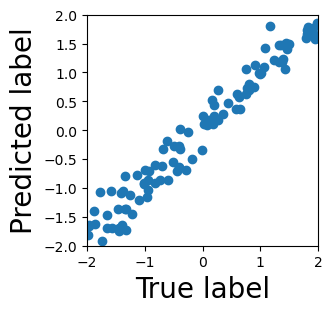
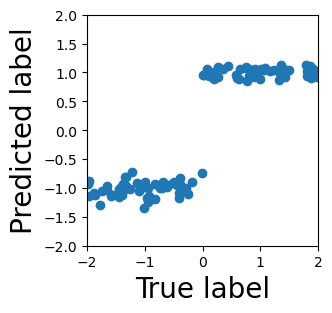
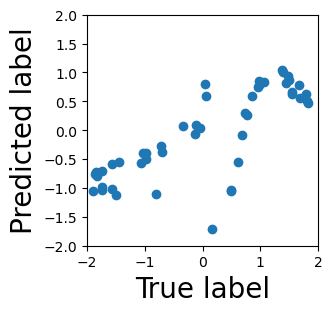
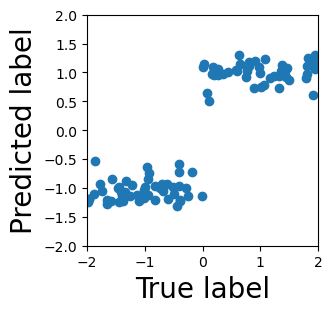
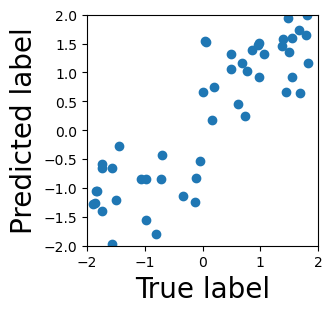
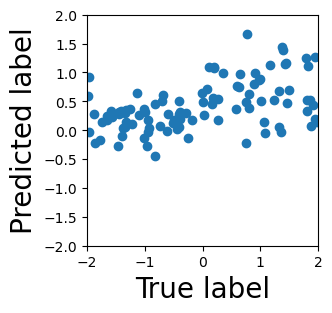
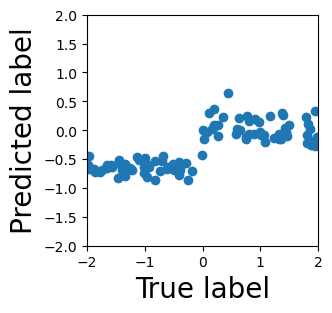
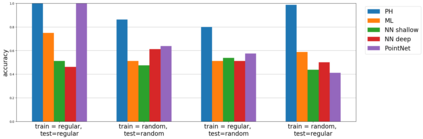
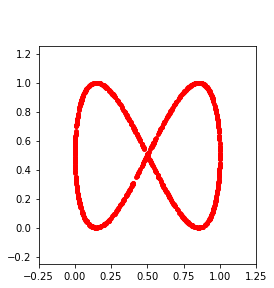
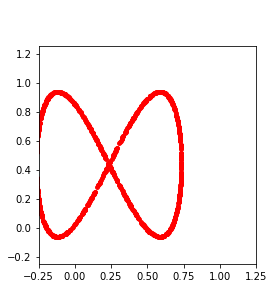
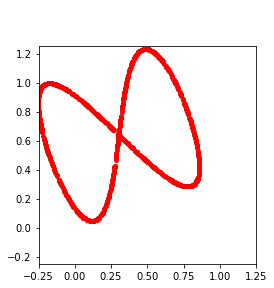
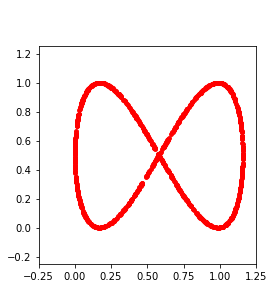
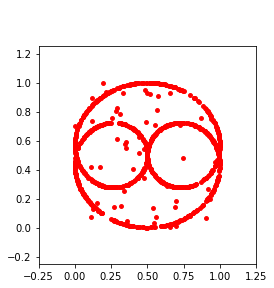
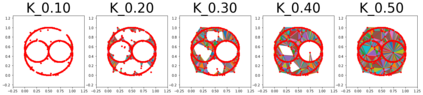
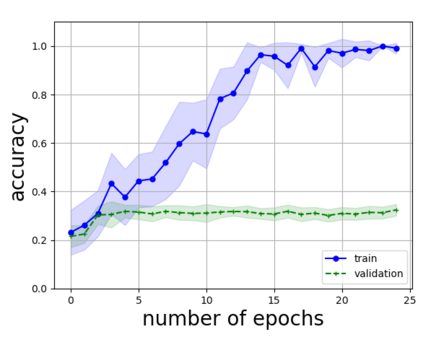
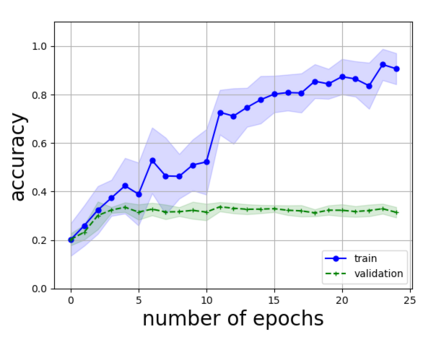
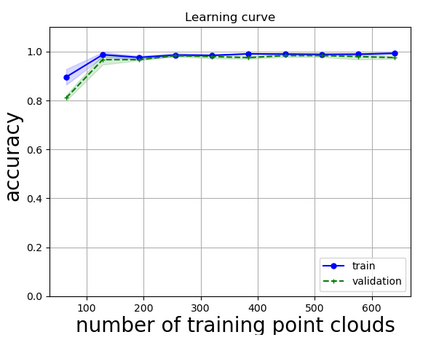
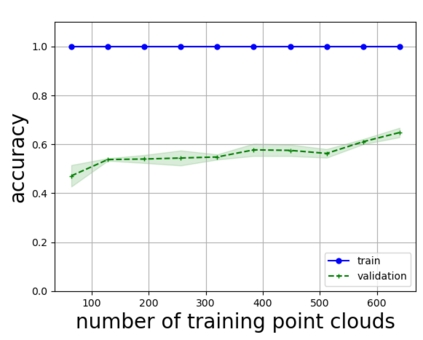
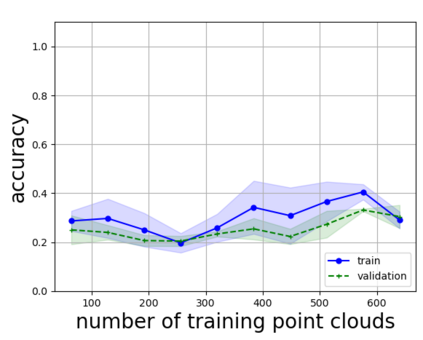
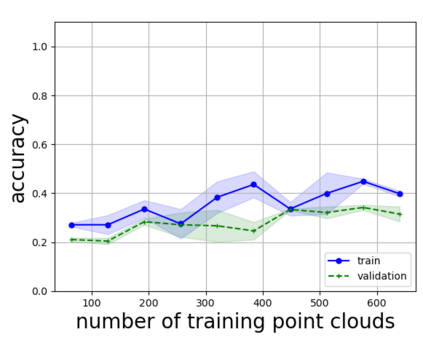
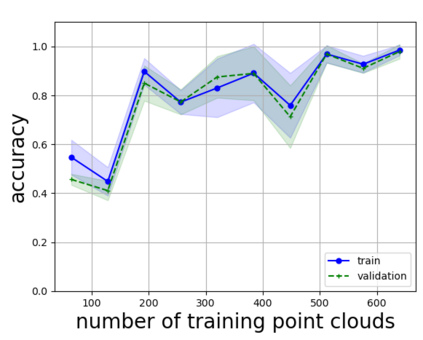
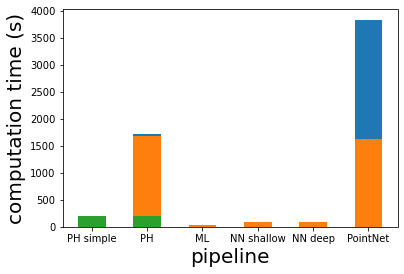
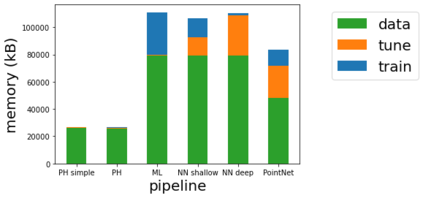
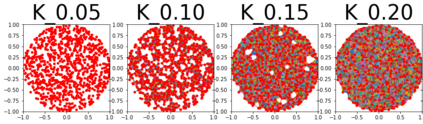
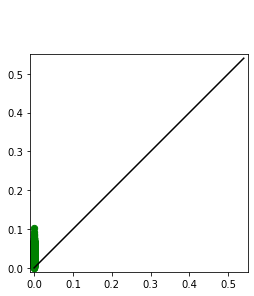
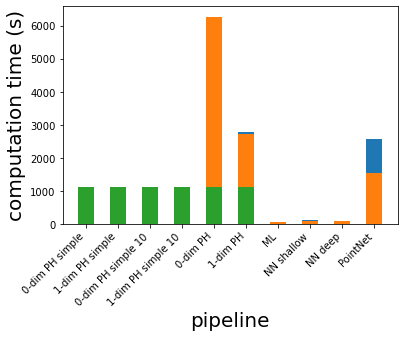
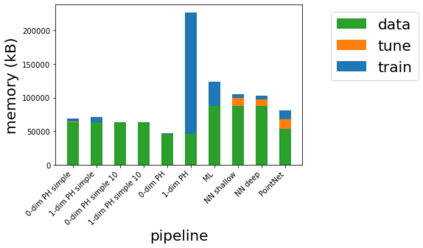
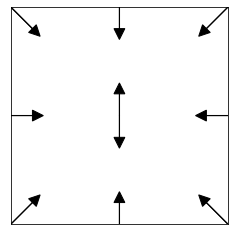
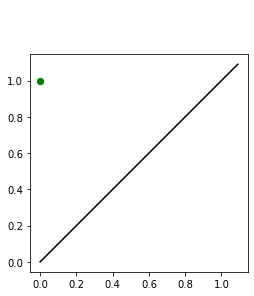
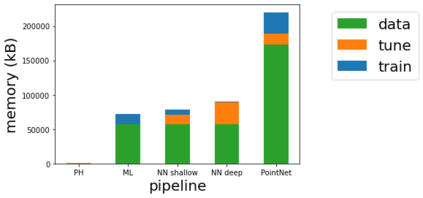
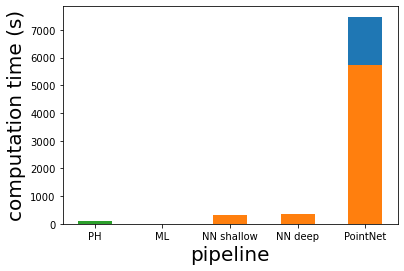
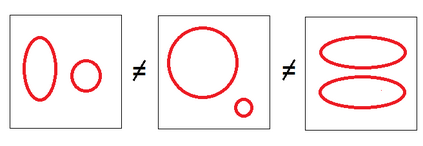
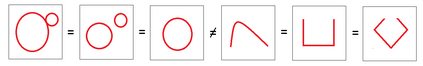Persistent homology (PH) is one of the most popular methods in Topological Data Analysis. While PH has been used in many different types of applications, the reasons behind its success remain elusive. In particular, it is not known for which classes of problems it is most effective, or to what extent it can detect geometric or topological features. The goal of this work is to identify some types of problems on which PH performs well or even better than other methods in data analysis. We consider three fundamental shape-analysis tasks: the detection of the number of holes, curvature and convexity from 2D and 3D point clouds sampled from shapes. Experiments demonstrate that PH is successful in these tasks, outperforming several baselines, including PointNet, an architecture inspired precisely by the properties of point clouds. In addition, we observe that PH remains effective for limited computational resources and limited training data, as well as out-of-distribution test data, including various data transformations and noise.
翻译:持久性同质学(PH)是地形学数据分析中最受欢迎的方法之一。虽然PH被用于许多不同类型的应用,但其成功的原因仍然难以找到。特别是,不知道PH在哪些类别的问题上最为有效,或者它在多大程度上能够探测到几何或地貌特征。这项工作的目标是查明PH在数据分析方面表现良好或甚至比其他方法更好的某些类型的问题。我们考虑三项基本的形状分析任务:探测从形状中取样的2D和3D点云的洞洞、弯曲和凝结数量。实验表明PH在这些任务中取得了成功,超过几个基线,包括点网,这是精确受点云特性启发的结构。此外,我们注意到PH对于有限的计算资源和有限的培训数据,以及包括各种数据转换和噪音在内的分配外测试数据仍然有效。