Fast convergent PML method for scattering with periodic surfaces: the exceptional case

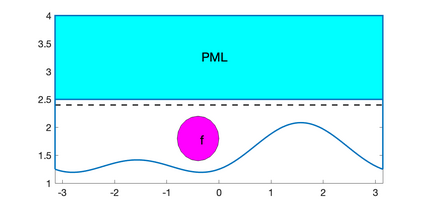
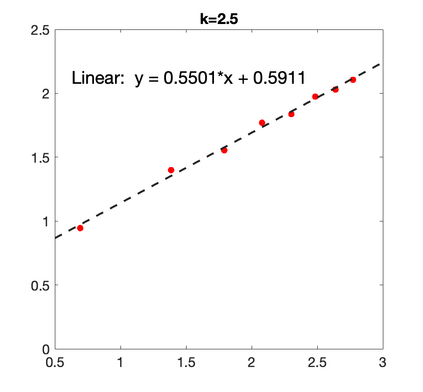
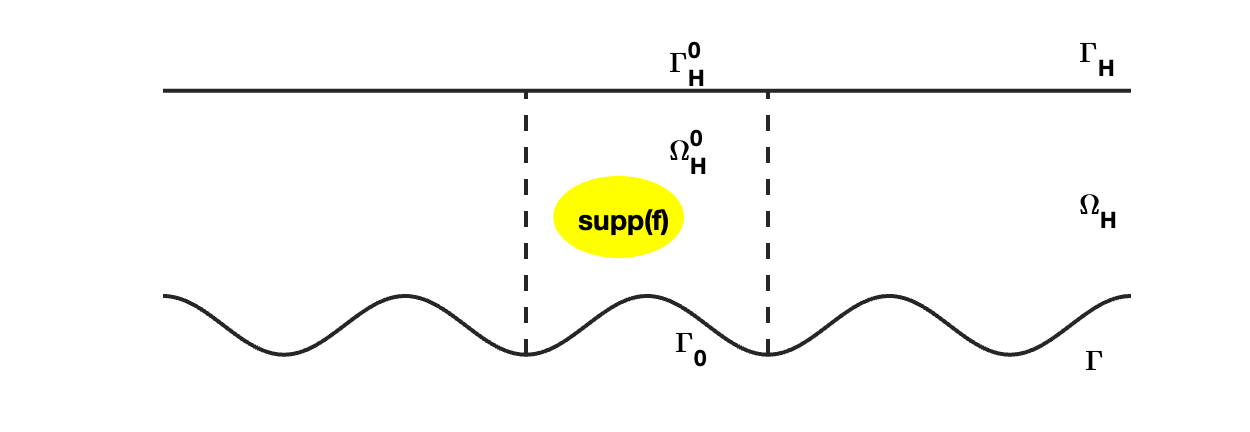
In the author's previous paper (Zhang et al. 2022), exponential convergence was proved for the perfectly matched layers (PML) approximation of scattering problems with periodic surfaces in 2D. However, due to the overlapping of singularities, an exceptional case, i.e., when the wave number is a half integer, has to be excluded in the proof. However, numerical results for these cases still have fast convergence rate and this motivates us to go deeper into these cases. In this paper, we focus on these cases and prove that the fast convergence result for the discretized form. Numerical examples are also presented to support our theoretical results.