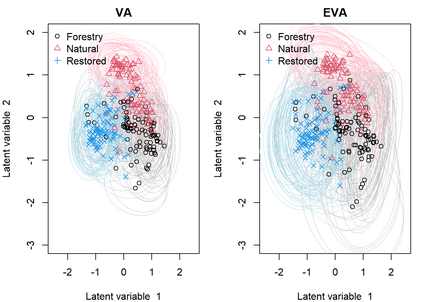
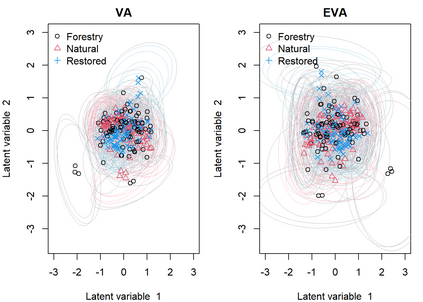
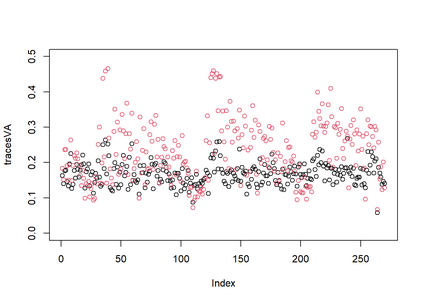
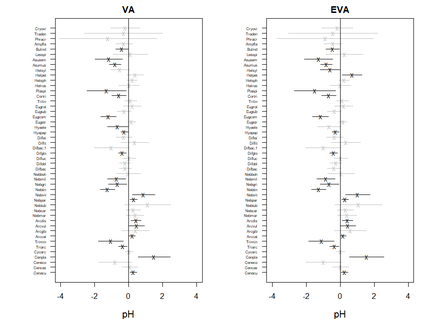
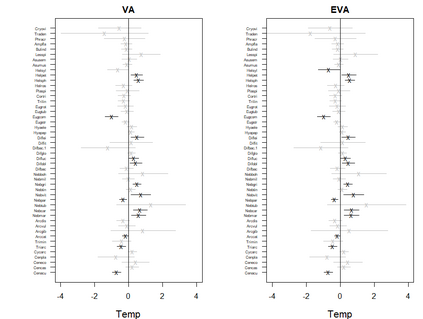
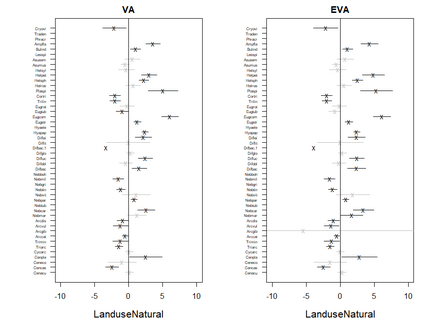
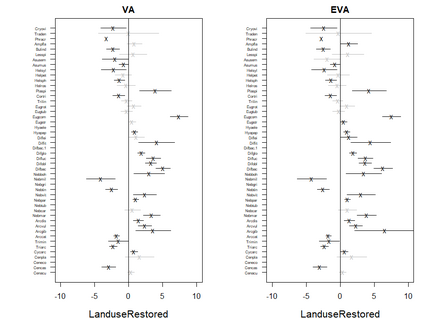
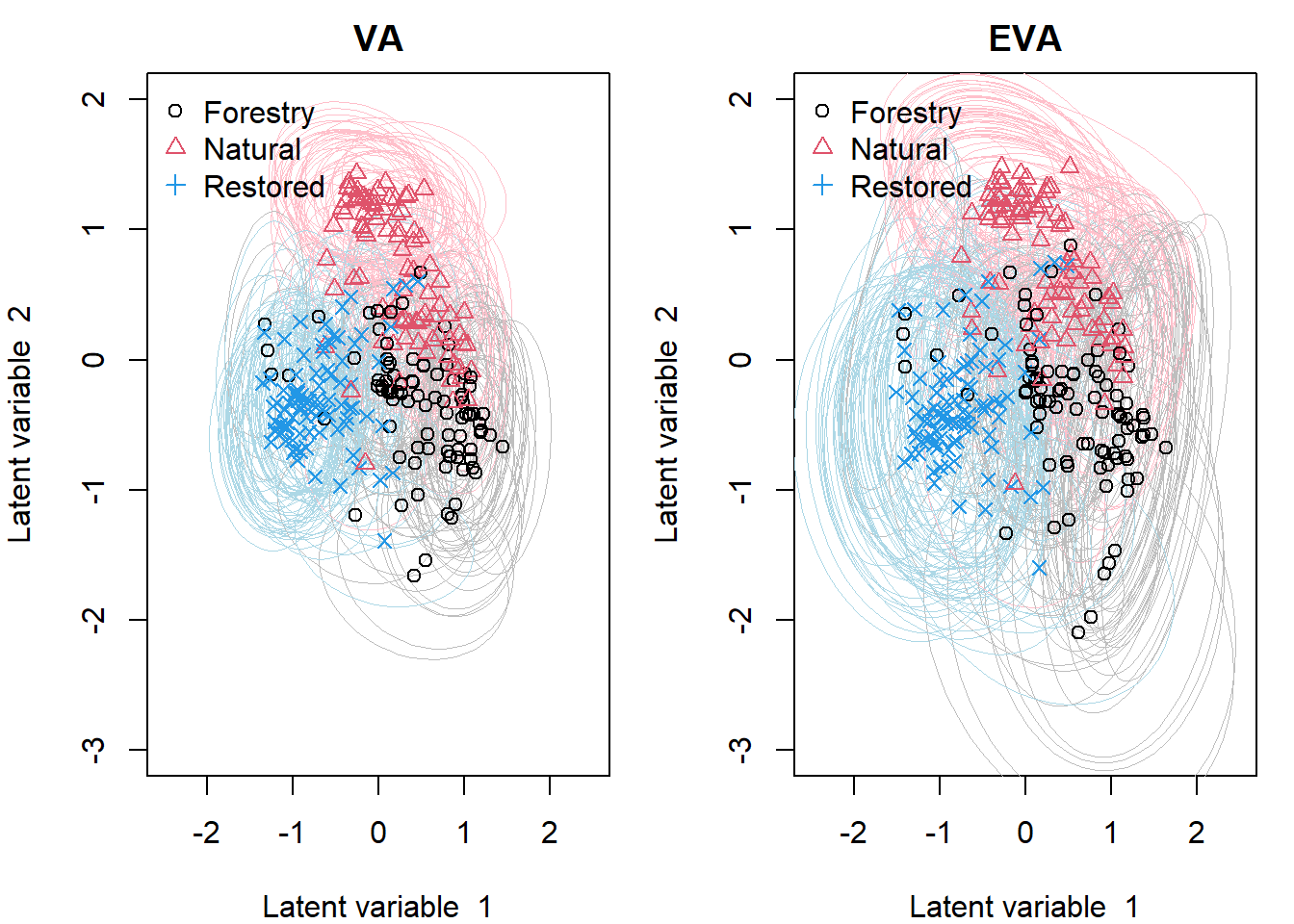
Generalized linear latent variable models (GLLVMs) are a class of methods for analyzing multi-response data which has garnered considerable popularity in recent years, for example, in the analysis of multivariate abundance data in ecology. One of the main features of GLLVMs is their capacity to handle a variety of responses types, such as (overdispersed) counts, binomial responses, (semi-)continuous, and proportions data. On the other hand, the introduction of underlying latent variables presents some major computational challenges, as the resulting marginal likelihood function involves an intractable integral for non-normally distributed responses. This has spurred research into approximation methods to overcome this integral, with a recent and particularly computationally scalable one being that of variational approximations (VA). However, research into the use of VA of GLLVMs and related models has been hampered by the fact that closed-form approximations have only been obtained for certain pairs of response distributions and link functions. In this article, we propose an extended variational approximations (EVA) approach which widens the set of VA-applicable GLLVMs drastically. EVA draws inspiration from the underlying idea of Laplace approximations: by replacing the complete-data likelihood function with its second order Taylor approximation about the mean of the variational distribution, we can obtain a closed-form approximation to the marginal likelihood of the GLLVM for any response type and link function. Through simulation studies and an application to testate amoebae data set in ecology, we demonstrate how EVA results in a universal approach to fitting GLLVMs, which remains competitive in terms of estimation and inferential performance relative to both standard VA and a Laplace approximation approach, while being computationally more scalable than both in practice.
翻译:普通线性潜伏变量模型(GLLVMS)是分析多反应数据的一种方法,近年来在分析生态中多变量丰度数据方面受到相当广泛的欢迎。GLLVMS的主要特征之一是能够处理多种类型的响应,例如(过度分散的)计数、二进制反应、(半-)连续的和比例数据。另一方面,引入潜在的潜在变量带来了一些重大的计算挑战,因为由此产生的可能性功能对于非正常分布的响应来说是一个棘手的组成部分。这刺激了对近似方法的研究,以克服这一整体的多变量数据。GLLLLVMMS的主要特征之一是它们能够处理各种类型的响应,例如(过度分散的)计数、二进制(半)和比例数据。另一方面,引入某些对响应分布和连接功能的组合,我们提出了一种扩大变异方法(EVA)方法,它能够将VA-A的测位应用范围扩大为整体整体,在GLLVMA的精确度数据序列中,我们用GLLVMA的精确的测算的精确性变数功能可以取代GLVA的精确的精确的测序。在GVA的测算中,在GVA的测序中,而任何的测算中,我们能的精确的精确的测算的精确的精确的测算的测算的精确的精确的测值的测值的测算值的测算法,在GVVVVVVVVA的精确性能的测值函数的精确性能功能中可以继续用。