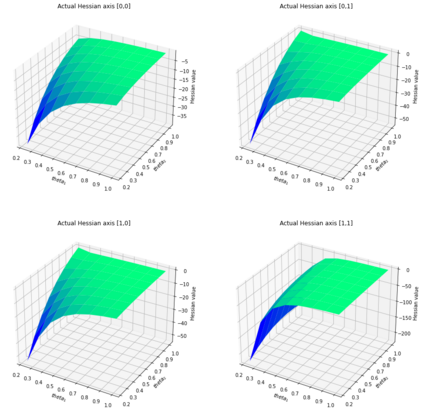
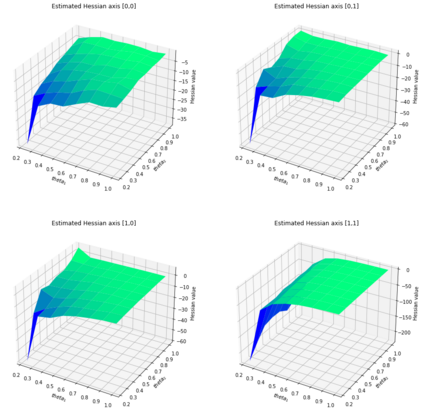
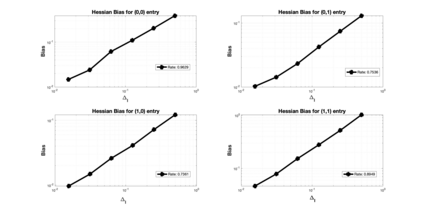
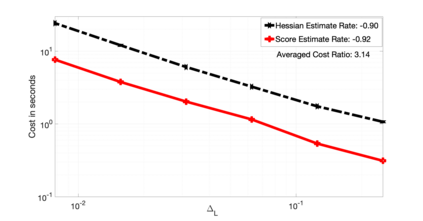
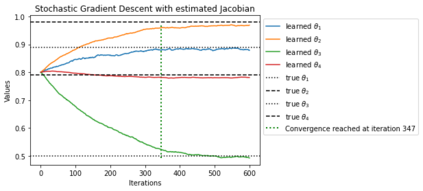
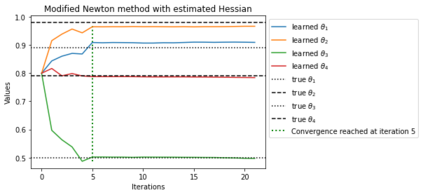
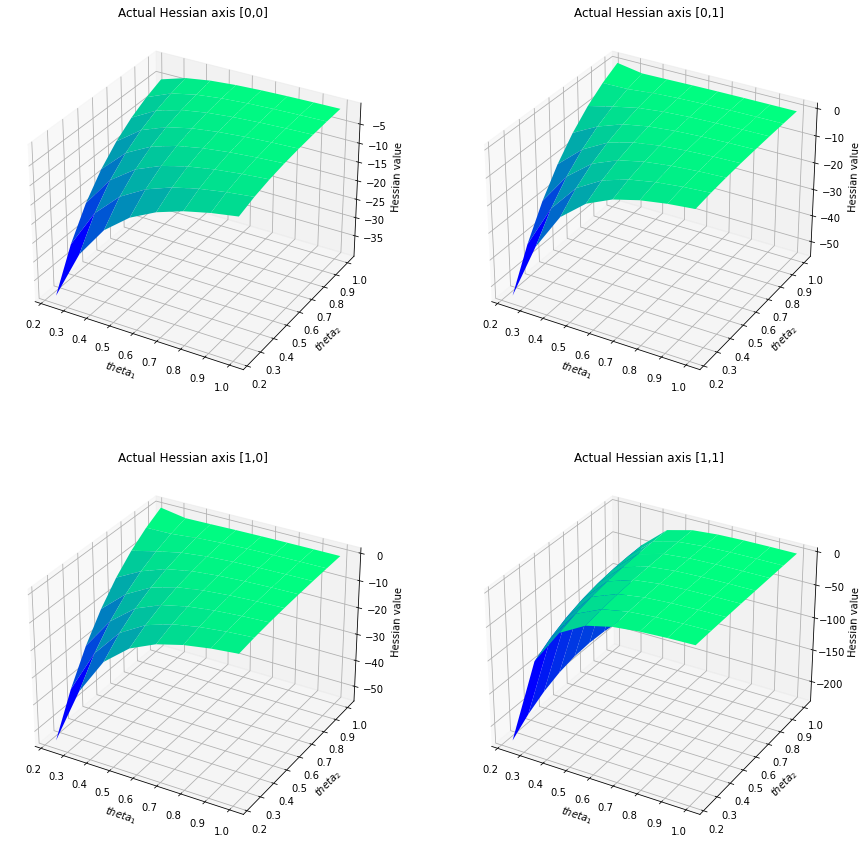
In this article we consider the development of unbiased estimators of the Hessian, of the log-likelihood function with respect to parameters, for partially observed diffusion processes. These processes arise in numerous applications, where such diffusions require derivative information, either through the Jacobian or Hessian matrix. As time-discretizations of diffusions induce a bias, we provide an unbiased estimator of the Hessian. This is based on using Girsanov's Theorem and randomization schemes developed through Mcleish [2011] and Rhee & Glynn [2015]. We demonstrate our developed estimator of the Hessian is unbiased, and one of finite variance. We numerically test and verify this by comparing the methodology here to that of a newly proposed particle filtering methodology. We test this on a range of diffusion models, which include different Ornstein--Uhlenbeck processes and the Fitzhugh--Nagumo model, arising in neuroscience.
翻译:在本文中,我们考虑为部分观测到的传播过程开发赫森人对参数的日志类函数的公正估计,这些过程产生于许多应用,在这些应用中,这种扩散需要衍生信息,通过雅各或赫森矩阵进行。作为扩散的时间分解导致偏差,我们为赫森人提供一个公正的估计。这是基于使用Girsanov的理论和通过Mcleish(2011年)和Rhee & Glynn [2015年)开发的随机化计划。我们展示了我们开发的赫森人估算师是不偏不倚的,并且是有限的差异之一。我们通过将此处的方法与新提议的粒子过滤方法进行比较来进行数字测试和核实。我们用一系列的扩散模型测试这一点,其中包括神经科学中产生的不同的Ornstein-Uhlenbeck过程和Fitzhugh-Nagumo模型。