Understanding the Relationship between Over-smoothing and Over-squashing in Graph Neural Networks

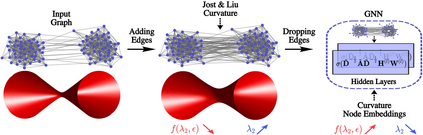
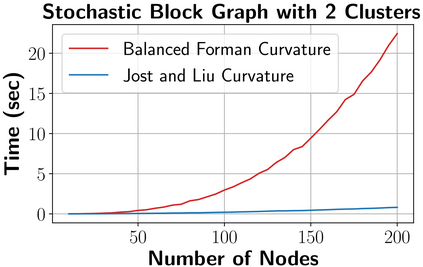
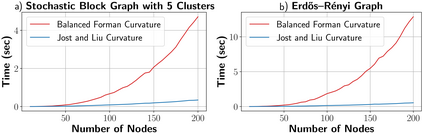
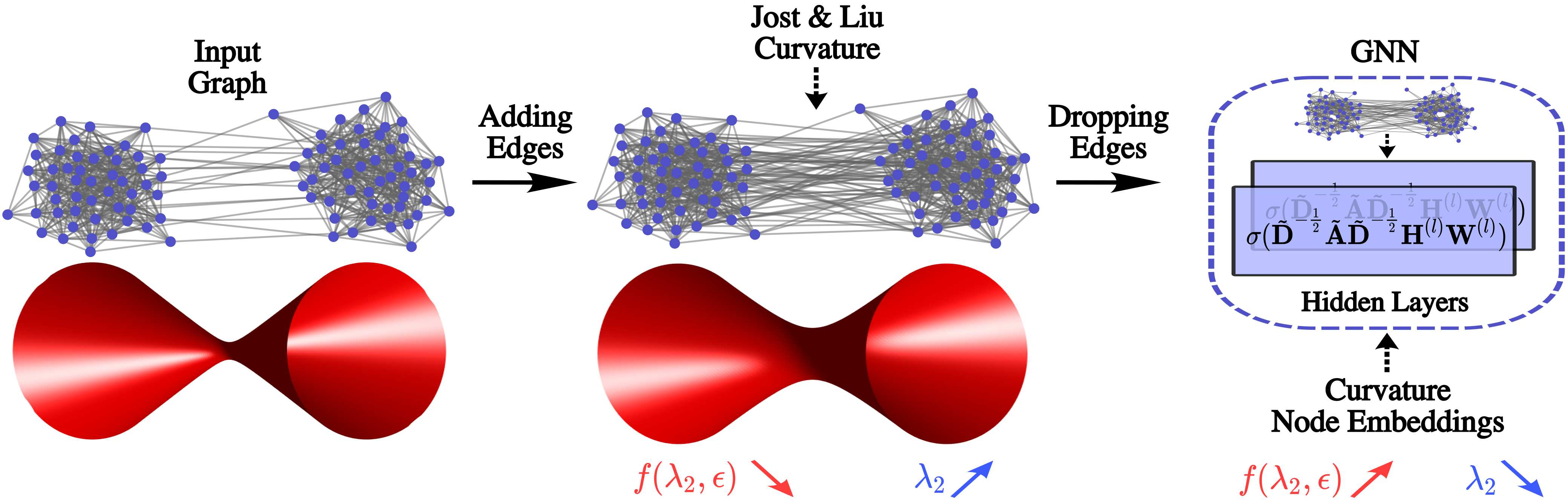
Graph Neural Networks (GNNs) have been successfully applied in many applications in computer sciences. Despite the success of deep learning architectures in other domains, deep GNNs still underperform their shallow counterparts. There are many open questions about deep GNNs, but over-smoothing and over-squashing are perhaps the most intriguing issues. When stacking multiple graph convolutional layers, the over-smoothing and over-squashing problems arise and have been defined as the inability of GNNs to learn deep representations and propagate information from distant nodes, respectively. Even though the widespread definitions of both problems are similar, these phenomena have been studied independently. This work strives to understand the underlying relationship between over-smoothing and over-squashing from a topological perspective. We show that both problems are intrinsically related to the spectral gap of the Laplacian of the graph. Therefore, there is a trade-off between these two problems, i.e., we cannot simultaneously alleviate both over-smoothing and over-squashing. We also propose a Stochastic Jost and Liu curvature Rewiring (SJLR) algorithm based on a bound of the Ollivier's Ricci curvature. SJLR is less expensive than previous curvature-based rewiring methods while retaining fundamental properties. Finally, we perform a thorough comparison of SJLR with previous techniques to alleviate over-smoothing or over-squashing, seeking to gain a better understanding of both problems.