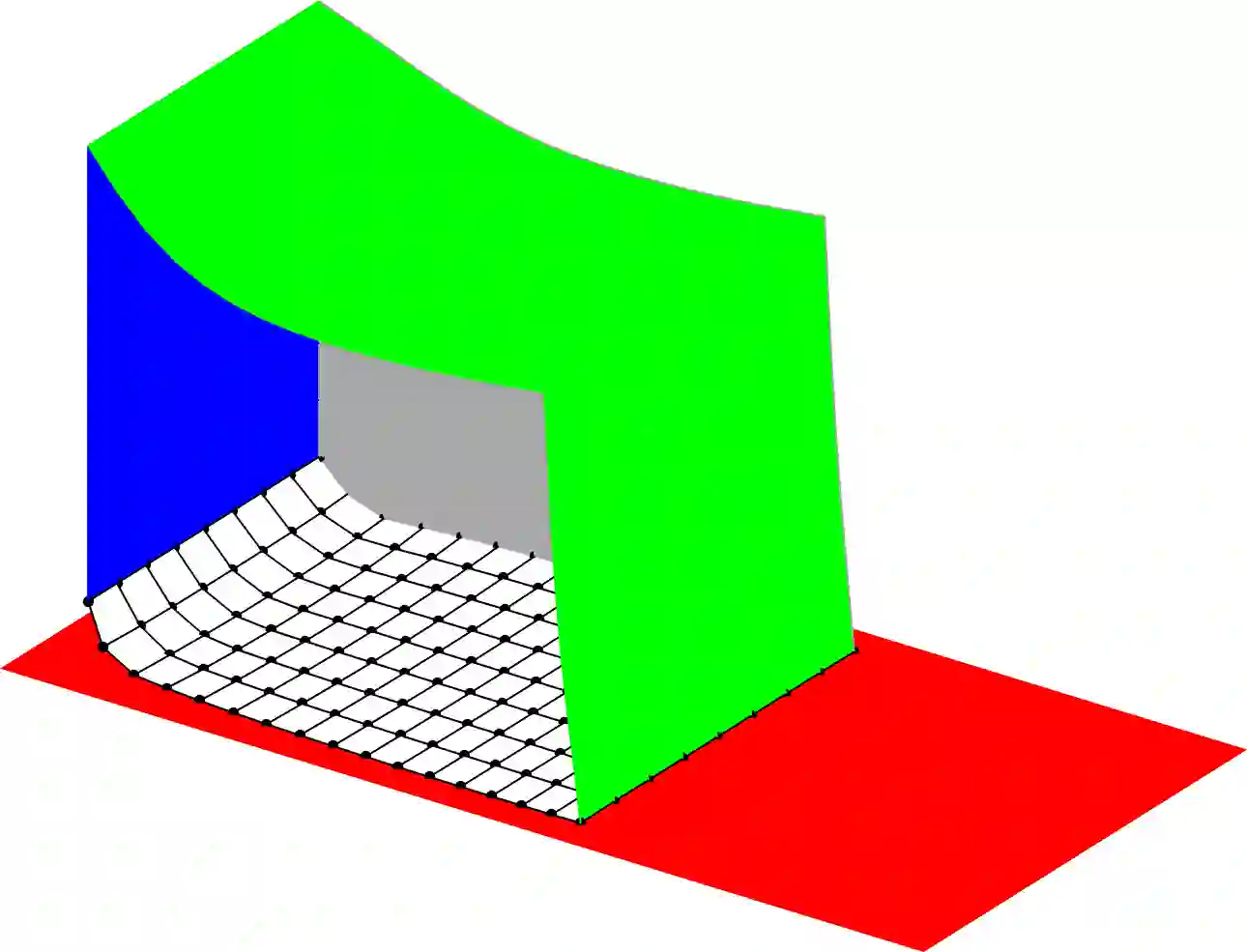
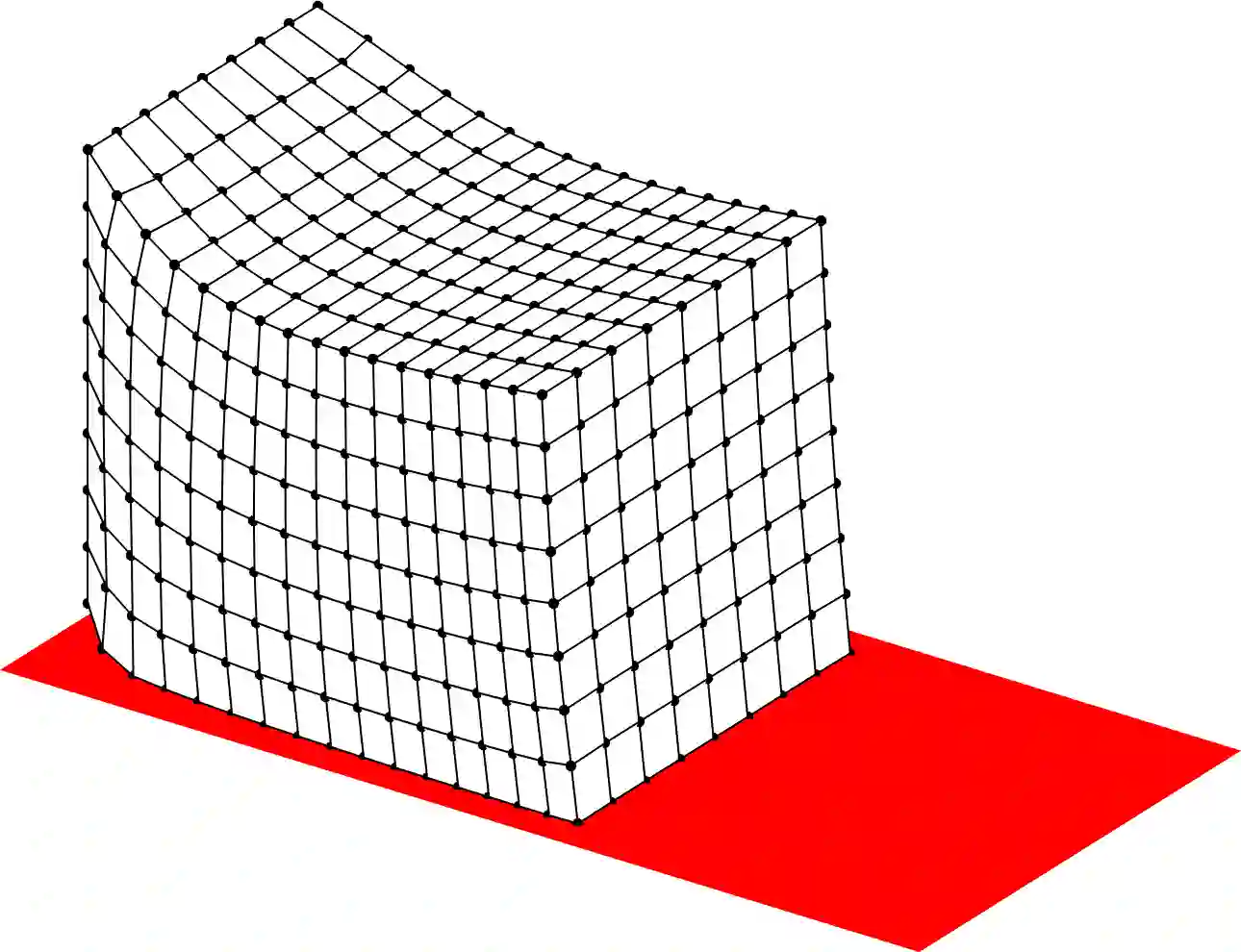
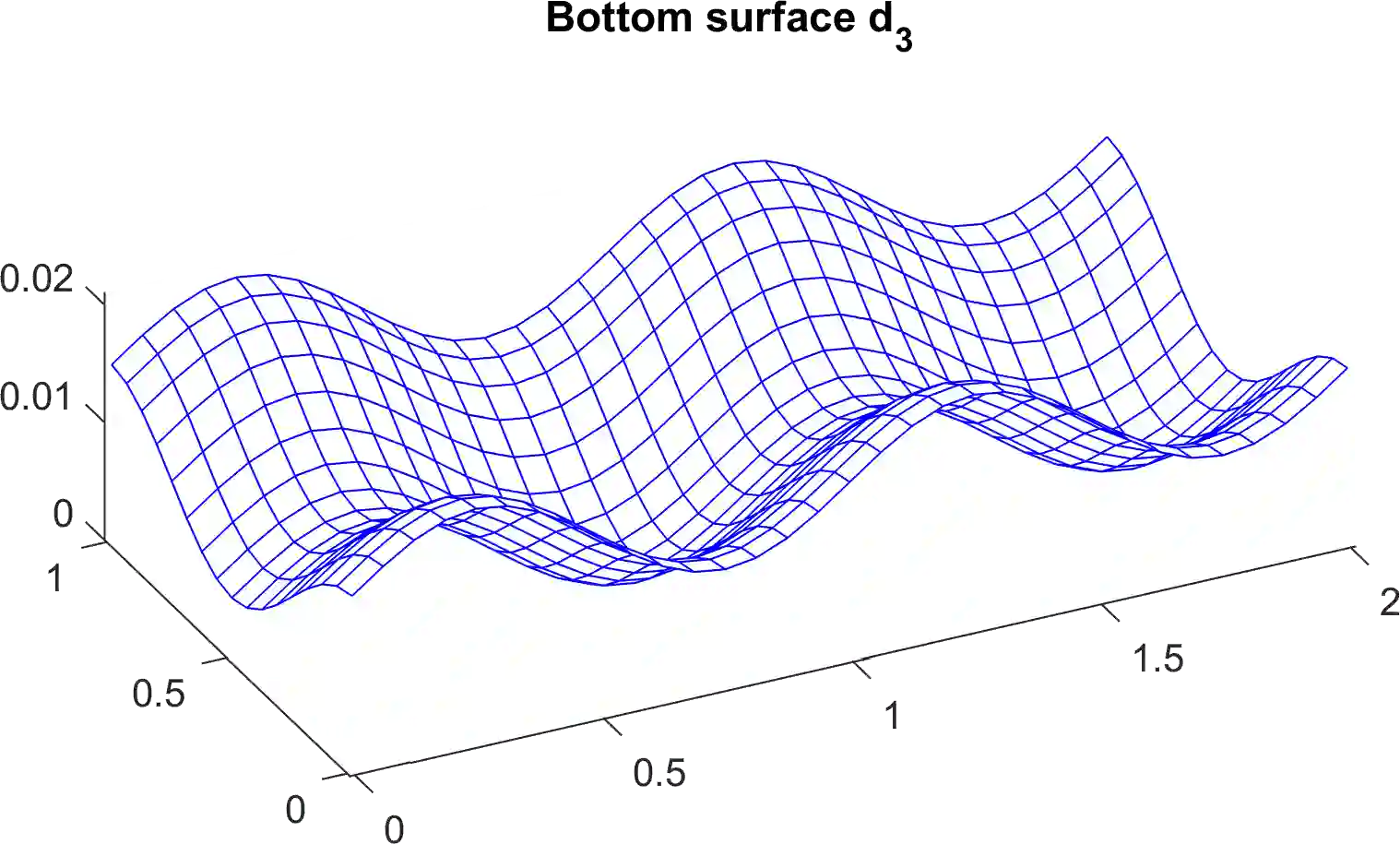
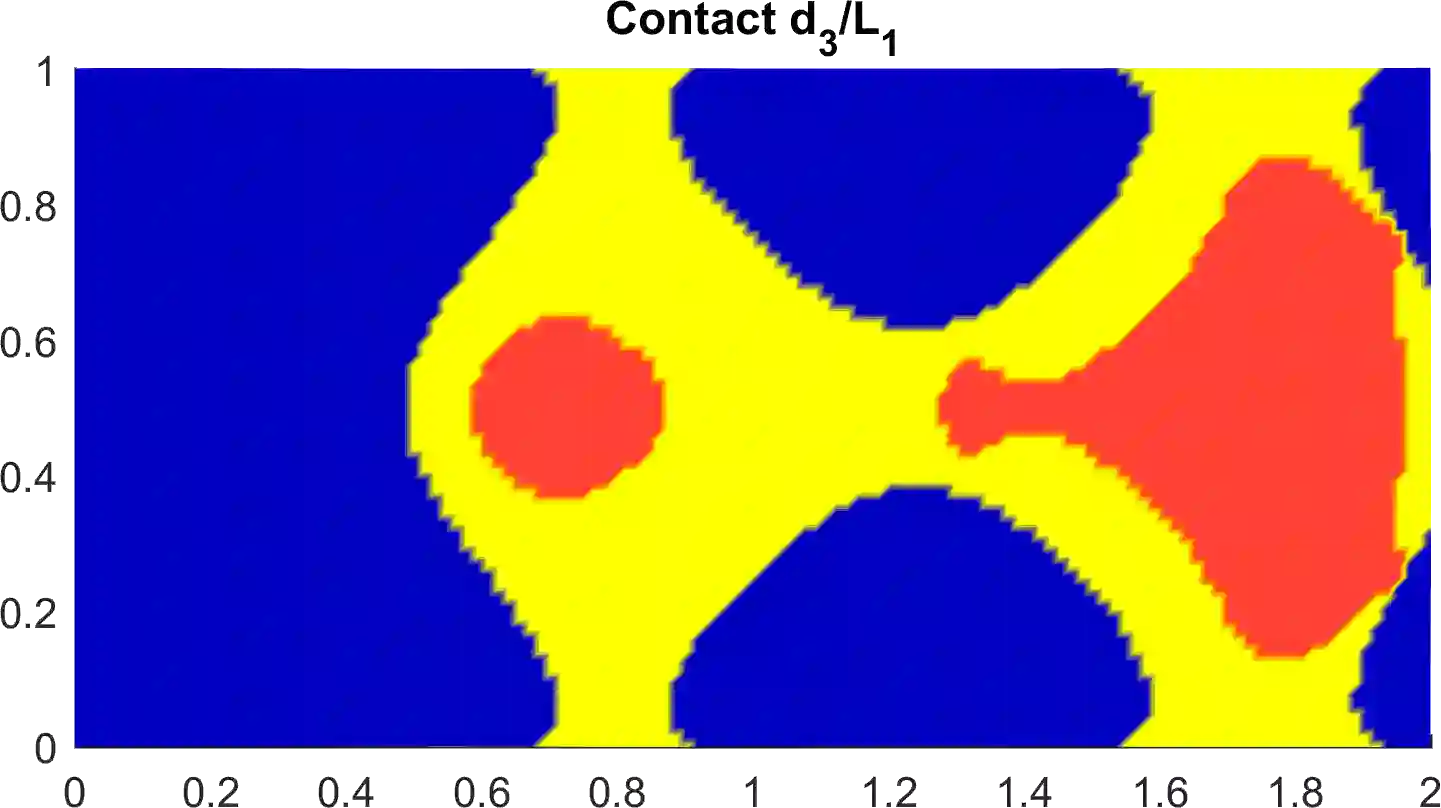
In the paper, a variant of the \ssstar Newton method is developed for the numerical solution of generalized equations, in which the multi-valued part is a so-called SCD (subspace containing derivative) mapping. Under a rather mild regularity requirement, the method exhibits (locally) superlinear convergence behavior. From the main conceptual algorithm, two implementable variants are derived whose efficiency is tested via a generalized equation modeling a discretized static contact problem with Coulomb friction.
翻译：在论文中,为通用方程式的数字解析方法开发了“ssstar Newton”法的变体,其中多值部分是所谓的SCD(含有衍生物的子空间)映射。根据比较温和的常规性要求,方法展示(局部)超线性趋同行为。从主要的概念算法中,得出了两种可执行的变体,其效率通过一个通用方程式模型,对库伦摩擦的离散静态接触问题进行测试。
相关内容
Arxiv
0+阅读 · 2022年7月16日
Arxiv
0+阅读 · 2022年7月15日
Arxiv
0+阅读 · 2022年7月15日
Arxiv
0+阅读 · 2022年7月14日
Arxiv
0+阅读 · 2022年7月13日
相关VIP内容
相关资讯
相关论文
Arxiv
0+阅读 · 2022年7月16日
Arxiv
0+阅读 · 2022年7月15日
Arxiv
0+阅读 · 2022年7月15日
Arxiv
0+阅读 · 2022年7月14日
Arxiv
0+阅读 · 2022年7月13日
微信扫码咨询专知VIP会员